1. 서 론
2. 수치해석 방법
2.1 수치해석 모델
2.2 시뮬레이션 설정 및 경계조건
2.3 지배방정식 및 난류모델 선정
3. 시뮬레이션 결과
3.1 열전달 성능
3.2 압력강하
3.3 열전달 성능계수
4. Nusselt Number (Nu)와 Friction factor (f) 상관관계
4.1 Nusselt Number(Nu)
4.2 Friction factor (f)
5. 결 론
1. 서 론
건축물은 국가 온실가스 배출의 16.6%, 에너지 소비의 20%를 차지하고 있어 국가 에너지 수요관리의 주 대상으로 인식되고 있다. 이에 따라 2025년부터 적용되는 민간건축물 제로에너지건축물 인증 의무화 정책이 시행되면서, 신재생에너지 사용이 필수적이며 그 중 유지설비가 간편한 태양광 시스템의 관심 또한 높아지고 있다.
하지만 태양광 시스템의 경우, 태양광 모듈에 일사가 유입되면 태양광 모듈의 표면 온도가 상승하여 발전효율이 감소하는 문제점이 있다. 이를 해결하기 위해 태양광 모듈에 공기 혹은 물을 흘려보내 태양전지를 냉각시켜 모듈의 발전효율 저감을 방지함과 동시에 열원을 획득하는 태양광/열 집열기에 관한 연구가 진행되어왔다. 태양광/열 집열기 중 공기식은 액체식보다 설비 및 유지보수가 간편하다는 장점이 있지만, 열전달 성능이 액체식에 비해 비교적 낮다는 단점이 있다. 따라서 공기식 태양광/열 집열기의 열전달 성능을 증가시키는 것은 매우 중요하다.
열전달 성능을 증가시키는 방법에는 열전달 면적을 증가시키는 방법과 유체의 난류를 촉진하여 공기의 열전달 계수를 증가시키는 방법이 있다. 열전달 면적을 증가시키는 방법에는 핀을 부착하거나 확장표면을 부착하는 방법 등이 있으며, 유체의 난류를 촉진시키는 방법에는 저항체 등을 열전달 표면에 부착하여 난류를 형성시키는 립 혹은 난류촉진제를 사용하거나, 덕트 배면이나 덕트 측면측에 부착하는 배플 혹은 블록등을 사용한다. 이러한 다양한 방법을 이용하여 공기식 태양광/ 집열기의 성능을 향상하는 연구들이 지속해서 진행됐다.
Alam et al.1)은 Protrusion rib을 태양광열 모듈 뒤편에 부착한 후 상대높이, 온도증가량, 레이놀즈 수, 상대 설치간격 등을 변경시키며 성능을 평가하였다. Ahn and Kim2,3)은 Computational fluid dynamics (CFD)를 사용하여 공기식 태양열 집열기에 T자형 저항체를 태양광 모듈 뒤편에 부착하였다. 그리고 추가적으로 Y자형 리브가 부착된 태양열 공기가열기의 열전달성능을 CFD 해석으로 평가하였다. Choi et al.4,5,6)은 태양광열 집열기 덕트부에 삼각형 립을 설치하여 CFD로 해석을 진행하고 추가적인 연구를 통해 실험 및 수치모델을 제작하여 다양한 조건에서의 성능 분석을 진행하였다. Singh et al.7)는 CFD를 사용하여 사각형, 원, 사다리꼴, 톱날 형상을 가진 립을 공기식 태양열 집열기에 부착하여 해석하였으며, Trapezoidal rib일 때 최대 3.58배 증가하였다.
Kim et al.8)는 CFD 해석을 통해 점점 배로 증가하는 공기식 태양광/열 집열기 내 반원 난류촉진제 형상조건 및 유동 조건에 따른 성능 평가를 진행하였다. Kim and Boo9)는 태양열 집열기의 흡수평판에 돌출형 삼각 개구부를 설치하여 열전달 성능을 실험으로 평가하였으며, 집열효율이 증가하는 것을 확인하였다. Ahn et al.10)는 곡선형 집열 베플이 부착된 공기식 태양광열 집열기를 실험을 통해 성능을 평가하였으며, 연간 성능에 대해서도 시뮬레이션을 통하여 분석했다. Kumar and Kim11)은 V형 립과 dimple로 구성된 공기식 태양열 집열기의 열성능을 평가하였다. Moon et al.12)은 ANSYS Fluent를 사용하여 공기식 태양광/열 집열기에 삼각형 립을 Re = 8000인 조건에서 해석을 진행하였다. 이 말고도 다양한 형상 조건에 따른 연구도 많이 진행되어왔다13).
그러나 앞선 연구들 및 본 연구의 선행연구12)에서는 난류 촉진제 형상에 따른 열전달 성능향상 및 압력강하에 대한 성능평가만 수행하는 한계를 가지며, 각각 제시한 난류 촉진제에 대한 최적 형상조건이나 다양한 유동 조건 및 난류 촉진제 형상조건에 따른 상관관계 분석 연구는 이루어지지 않았다.
따라서 본 연구에서는 태양광/열 집열기 내 비균일 삼각 단면을 갖는 난류 촉진제의 형상조건 및 유동 조건에 대한 열전달 성능 및 압력강하를 평가하고, 난류 촉진제 형상조건 및 공기의 유동 조건에 따른 Nusselt number (Nu) 및 Friction factor (f)의 상관관계식을 제시하였다. 향후 본 연구에서 제시한 상관관계식을 바탕으로 난류촉진제의 최적 형상조건을 제시하여, 고효율 태양광/열 집열기 설계를 위한 기초자료로 사용하고자 한다.
2. 수치해석 방법
2.1 수치해석 모델
태양광/열 집열기는 Fig. 1와 같이 설계하여 수치해석을 진행하였다. 태양광 패널 후면부에 비균일 삼각 단면을 갖는 난류 촉진제를 부착하였으며, 공기 덕트는 단열조건으로 태양광 패널 하부에 만들었다. 난류 촉진제는 Fig. 2와 같이 정면에서 봤을 때, 공기의 유동 방향과 수직 방향으로 삼각형 형상을 가지며, 측면에서 보았을 땐 사각형 형상을 가진다.
Fig. 3처럼 태양광/열 집열기는 너비(W) 400 mm, 덕트 높이(H) 50 mm, 총 덕트 길이(L) 1,542 mm로 설계하였으며, 덕트 길이 중 난류 촉진제가 부착된 태양광 모듈 길이는 480 mm이다. 태양광/열 집열기 시뮬레이션 모델의 입구 측 길이는 708 mm, 출구 측 길이는 354 mm로 설계하였다. 이는 시뮬레이션의 정확성을 높이기 위해 ‘ASHRAE standard 93-2002’14)에서 제시한 덕트 최소 길이인 입구 측 , 출구 측 의 지침을 따라 설계하였다.
난류 촉진제 형상조건은 높이(e), 설치간격(p), 폭(w)를 변경하며 해석 수행을 진행하였으며, 상대높이(e/h), 상대설치간격(p/e), 상대폭(w/e)과 같이 무차원수로 변환하여 형상조건에 대한 성능을 평가하였다5). 난류 촉진제 형상조건 총 36가지를 변화하면서 해석하였으며, 태양광/열 집열기 및 난류촉진제의 세부 형상조건은 Table 1, Table 2에 나타내었다.
Table 1
Shape conditions of PV/T collector
| Parameter | Value | |
| Duct length (mm) | Entrance | 708 |
| Test section | 480 | |
| Exit | 354 | |
| Duct width (mm) | 400 | |
| Duct height (mm) | 50 | |
Table 2
Geometric conditions of turbulator
2.2 시뮬레이션 설정 및 경계조건
태양광/열 집열기 내 난류 촉진제 시뮬레이션을 진행하기 위해 상용 CFD 소프트웨어인 ANSYS FLUENT 17.2를 사용하였다. 해석 간편화를 위해 실제 시뮬레이션 해석 수행 모델은 태양광/열 집열기 구조물 내 유동 채널을 묘사하여 모델링 하였다7).
격자는 Proximity and curvature로 설정하였으며, 격자 표면 최대 사이즈는 0.1846 mm로 설정한 후 나머지 사이즈는 기본값으로 설정하였다. 최종적으로 총 Cell 수는 형상조건에 따라 약 50만 ~ 200만 개의 값을 가졌다. 시뮬레이션 기본설정은 정상상태로 설정하였다. 해석 모델은 열전달 성능평가를 위하여 에너지 방정식을 사용하였다. 시뮬레이션 해석에 사용된 유체는 공기를 이용하며, 공기 온도는 300 K로 설정하였다. Table 3은 공기의 300 K일 때 물성값에 대하여 나타나 있다. Solution method는 Patankar에 의해 제안된 SIMPLE scheme15)로 하였으며, 시뮬레이션 계산 정확성을 높이기 위해 이차방정식으로 설정하였다.
Table 3
Air Properties
| Parameter | Value |
| Temperature (K) | 300 |
| Density (kg/m3) | 1.1771 |
| Specific heat (J/kg·K) | 1006.3 |
| Conductivity (W/m·K) | 2.6107 e-02 |
| Dynamic viscosity (kg/m·s) | 1.8531 e-05 |
| Prandtl number (-) | 0.7143 |
본 해석에서 상세 경계조건은 Table 4와 같으며, 태양광 모듈에 열 유속조건으로 1,000 W/m2로 설정하였다. 참고문헌3,4,5,6)을 바탕으로 유동 조건은 4가지로 Re = 3000 ~ 18000범위에서 진행하였으며, 식(1)을 사용하여 0.5313 ~ 4.0735 m/s 범위의 공기 유속 4가지 조건을 설정하였다.
사각 덕트에 대한 수력직경(Hydraulic diameter)은 식(2)을 사용하여 0.089 m로 설정하였다.
Turbulence는 Intensity and hydraulic diameter에서 Turbulent intensity는 식(3)을 사용하여 4.56 ~ 5.88%의 값을 설정하였다.
출구 측에는 압력조건으로 대기압인 101,325 Pa로 설정하였다. 나머지 공기유동층과 벽면 사이의 경계조건은 Stationary wall과 No slip shear condition으로 하였다.
Table 4
Boundary Conditions
본 시뮬레이션 결과의 정확성을 높이기 위해 Adaption gradiant를 이용하여 Temperature, Pressure, Velocity, Wall shear stress, Turbulence intensity 순으로 Mesh 수를 늘려가며, 시뮬레이션을 각각 5회 반복실행하였다. Table 5는 Re = 13000, e/h = 0.04, p/e = 6, w/e = 1인 조건에서, Adaption gradiant를 활용하여 확인한 Cell과 Nu 변화 값을 나타내었으며, 최종적으로 Nu 변화율이 1% 미만으로 감소하는 것을 확인하였다. 이는 Mesh 수를 추가로 증가하는 것이 시뮬레이션 결과값의 정확도에 미치는 영향이 미미하다고 판단되며, 본 연구에서 사용된 Mesh 구조가 신뢰할만하다고 판단하였다.
Table 5
Adaption information
2.3 지배방정식 및 난류모델 선정
태양광/열 집열기 내 난류 촉진제의 시뮬레이션 해석을 수행하였으며 연속방정식(4), 공기 유동해석을 위한 운동방정식(5), 열전달 조건을 위한 에너지 방정식(6)을 기초로 하였다16).
또한, 비압축성 기체의 정상상태 난류 모델을 해석하기 위해 적합한 난류 모델을 모색하였다. 다음 식(7)인 Dittus-Boelter equation8)을 사용하여 ANSYS FLUENT 내의 다양한 난류 모델 Nu 값과 비교 검증하였다.
다양한 난류 모델을 비교한 결과 Fig. 4와 같은 경향을 보였으며, k-ε Rng & enhanced wall treatment 난류 모델에서 평균 퍼센트 오차율 9.31%로 가장 작은 오차율을 보여 위 난류 모델을 선정하였다.
3. 시뮬레이션 결과
난류 촉진제의 열전달 성능 및 압력강하 CFD 해석 결과를 바탕으로 다음 식(8)과 식(9)을 이용하여 무차원수인 Nu 수와 f로 변환한 후 성능을 평가하였다.
3.1 열전달 성능
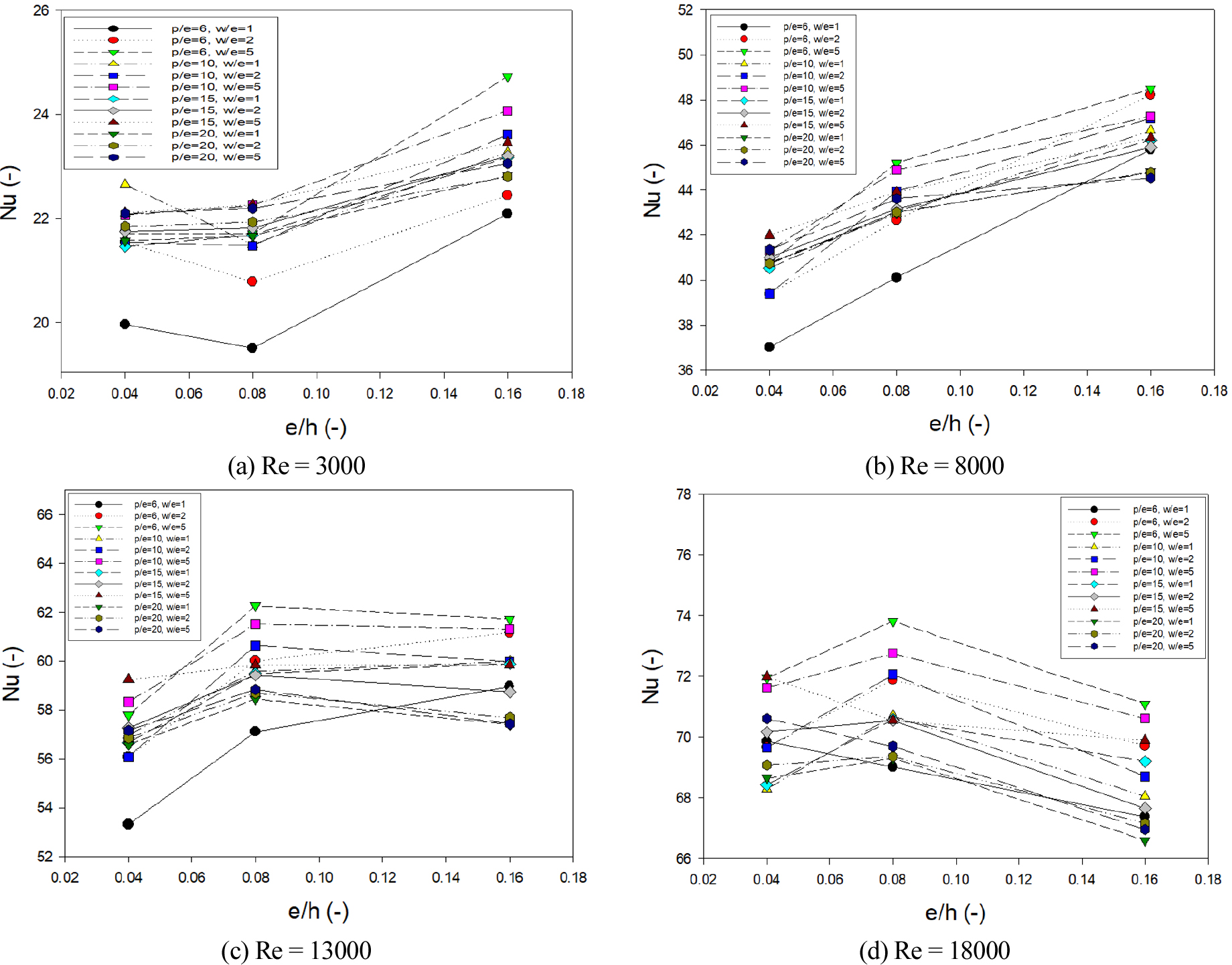
Fig. 5에서는 불균일 난류촉진제의 열전달 성능을 비교하기 위해 e/h에 대한 Nu 수를 나타낸 그래프이며, Re = 3000 ~ 18000 범위의 총 4가지로 구분하였다. 비교군은 w/e, p/e를 변경시키며 성능평가를 하였다. Re = 3000, e/h = 0.08, p/e = 6, w/e = 1인 조건에서, Nu = 19.51로 가장 낮게 측정되었으며, 이는 아무것도 설치되지 않은 덕트의 Nu 값인 Nus 에 비해 1.60배 증가하였다. 또한, Re = 18000, e/h = 0.08, p/e = 6, w/e = 5인 조건에서 Nu = 73.82로 가장 높게 측정되었으며 이는 Nus에 비해 1.33배 증가하였다. Re = 3000, e/h = 0.16, p/e = 6, w/e = 5인 조건에서 Nu = 24.73 이였으며, Nus에 비해 2.03배 증가한 값이며, 가장 큰 열전달 성능향상을 보였다.
Fig. 5와 같이 Re 수가 증가함에 따라 Nu 또한 선형적으로 증가함을 볼 수 있다. 이는 유속이 증가함에 따라 대류 열전달 계수가 증가하였기 때문이다. 그러나 Nu/Nus는 Re가 증가함에 따라 오히려 감소하는 것을 확인하였다. Fig. 5 (a)에서는 e/h = 0.04에서 Nu 감소하다가 0.08에서는 증가하는 경향성을 보이며, (b)에서는 e/h 증가에 따른 선형적으로 증가했으며, (c)와 (d)에서는 (a)와 반대로 0.04에서 증가하다가 0.08에서 Nu이 감소하는 것을 볼 수 있었다.
이는 유속조건과 e/h 사이의 열전달 성능과의 상관관계를 확인할 수 있다. Fig. 6은 p/e = 10, w/e = 2인 조건에서 e/h 및 Re에 따라 온도분포를 나타내었다. 유속조건이 느릴 경우 난류촉진제의 e/h가 높아야 열전달 성능이 향상되지만, 유속조건이 빠를 경우 e/h가 낮을 때 열전달 성능이 향상하였다. 낮은 Re 영역에서는 열 경계층이 두꺼워지므로 e/h가 높아야 열 경계층 파괴가 잘 일어났다. 또한, 높은 Re 영역에서는 열 경계층이 비교적 얇아지므로 e/h가 낮아야 열 경계층 파괴가 잘 일어나며, 오히려 e/h가 높으면 주 유동까지 방해하게 되어 열전달 성능이 낮아진다고 판단된다.
3.2 압력강하
Fig. 7에서는 불균일 난류촉진제의 압력강하 비교를 위해 e/h에 대한 f를 나타낸다. 비교군 및 유속조건은 위 Fig. 5와 같으며, e/h에 대한 f 경향성을 확인하였다.
Re = 3000, e/h = 0.16, p/e = 6, w/e = 1인 조건에서 f = 0.0501인 값을 보였으며, 이는 가장 큰 Friction factor 값이며, 이는 아무것도 설치되지 않은 덕트의 f 값인 fs 보다 4.68배 증가하였다. Re = 18000, e/h = 0.04, p/e = 20, w/e = 2인 조건에서 Friction factor = 0.0166인 값을 보였으며, 이는 가장 작은 Friction factor 값이며, fs 보다 2.4배 증가하였다.
Fig. 7에서는 공기 유속이 증가할수록 f는 감소하는 경향을 보인다. 또한, e/h가 증가할수록 f도 증가하였으며 이는 난류촉진제의 마찰 면적 증가로 인해 마찰계수가 증가했기 때문이다.
3.3 열전달 성능계수
공기 유동 채널에 난류촉진제를 설치 시 앞선 결과들로 열전달 성능이 향상한다는 것을 확인하였지만, 마찰계수 또한 증가하는 것을 확인할 수 있었다. 이처럼 마찰계수가 증가하면 송풍을 위한 팬의 동력이 증가하여 시스템의 에너지효율이 감소되는 문제점이 야기될 수 있다. 이러한 문제를 고려하기 위해 열전달 성능과 마찰계수를 종합적으로 평가할 수 있는 열전달 성능계수를 이용하였다. Webb and Eckert17)이 제시한 Thermal hydraulic performance parameter (THPP)를 사용하였으며, 그 식은 식(10)과 같다.
Fig. 8은 열전달 성능계수를 평가하기 위해 e/h에 대한 THPP를 나타낸 그래프이다. Re = 3000, e/h = 0.04, p/e = 10, w/e = 1인 조건에서 THPP = 1.22로 가장 높은값을 보였으며, Re = 18000, e/h = 0.16, p/e = 6, w/e = 1인 조건에서 THPP = 0.81로 가장 낮은 THPP 값임을 확인하였다. Fig. 7(a), (b)에서는 대체로 1 이상의 THPP값을 보였으며, (c)와 (d)에서는 1 이하의 값을 보였다. (a), (b)에서는 e/h에 대한 THPP 변화는 적었으며, (c)와 (d)에서는 e/h가 증가할수록 THPP는 감소하였다. 또한, THPP 에서는 e/h에 대한 변화량보다는 p/e에 대한 영향이 컸으며, p/e가 작을수록 THPP 또한 낮음을 확인할 수 있었다. 이러한 결과 및 경향성 등을 방정식으로 표현하기 위해 상관관계식을 제시하였다.
4. Nusselt Number (Nu)와 Friction factor (f) 상관관계
본 연구에서는 형상조건 및 유동 조건에 따라 Nu 변화 및 f 변화를 연구하였으며, 시뮬레이션 결과를 기초로 하여 형상조건 및 유동 조건에 대한 Nu 및 f에 대한 상관관계식을 제시하려고 한다. 상관관계식은 식(11)과 식(12) 와 같이 종속변수를 Nu, f로 지정하고, 독립변수는 Re, e/h, p/e, w/e로 설정하였다.
4.1 Nusselt Number(Nu)
독립변수에 따른 Nu의 변화를 상관관계 식으로 나타내기 위해, 독립변수(Re, e/h, p/e, w/e) 중 각각 차례로 상관관계식으로 나타내려 하며, 이는 log-log plot 기법을 이용하여 다음과 같은 순서대로 계산한다.
Nu과 Re의 상관식을 로그 그래프로 나타내면 Fig. 9와 같다.
ln(Re)-ln(Nu)의 기울기는 0.6454이므로 n = 0.6454이고, 식(13)에 대입하면 식(15)과 같이 나타난다.
위 식(15)에서 A0를 구하기 위해서 난류촉진제의 e/h, p/e, w/e의 열전달 성능 결과를 순차적으로 상관관계식을 만들어, 최종적으로 A0를 e/h, p/e, w/e에 대한 식을 제시하려 한다.
첫 번째로 e/h에 대한 상관식을 A0로 만들기 위해 시뮬레이션 결과값을 바탕으로 그래프에 추세선을 나타내면 다음 Fig. 10과 같다. 그래프는 위 방법과 같이 x-y 축 모두 로그 형태로 치환하여 표현하였으며, 오차를 줄이기 위하여 이차방정식으로 만들어 상관식을 만들었다.
Fig.10 으로부터 나온 결과값은 식(16)과 같으며, B0는 p/e, w/e 과의 상관식을 나타내기 위해 임의정수로 표현하였다.
식(16)을 A0에 대하여 정리한 후 식(17)을 식(15)에 대입하여 Nu에 대한 식으로 나타내면 다음 식(18)과 같다.
B0를 p/e에 대한 상관식을 만들기 위해 시뮬레이션 결과값으로 그래프를 그리면 Fig. 11와 같고, 그래프 추세선 식을 정리하면 식(19)과 같다.
따라서 식(20)을 식(18)에 대입하여 Nu에 대한 식으로 나타내면 식(21) 다음과 같다.
C0를 w/e에 대한 상관식을 만들기 위해 시뮬레이션 결과값을 바탕으로 그래프를 그리면 Fig. 12와 같고, 그래프 추세선 식을 정리하면 식(19)과 같다.
w/e는 일차방정식일 때 오차율이 더 낮아 다음 식(22)와 같이 1차 식으로 전개하였다.
이때, D0는 Fig. 11의 상수 결과값과 같이 0.092이며, 이를 식(22)에 대입하면 식(23)과 같다.
최종적으로 식(23)을 식(21)에 대입하여 Nu에 대한 식으로 나타내면 최종적으로 식(24)와 같다.
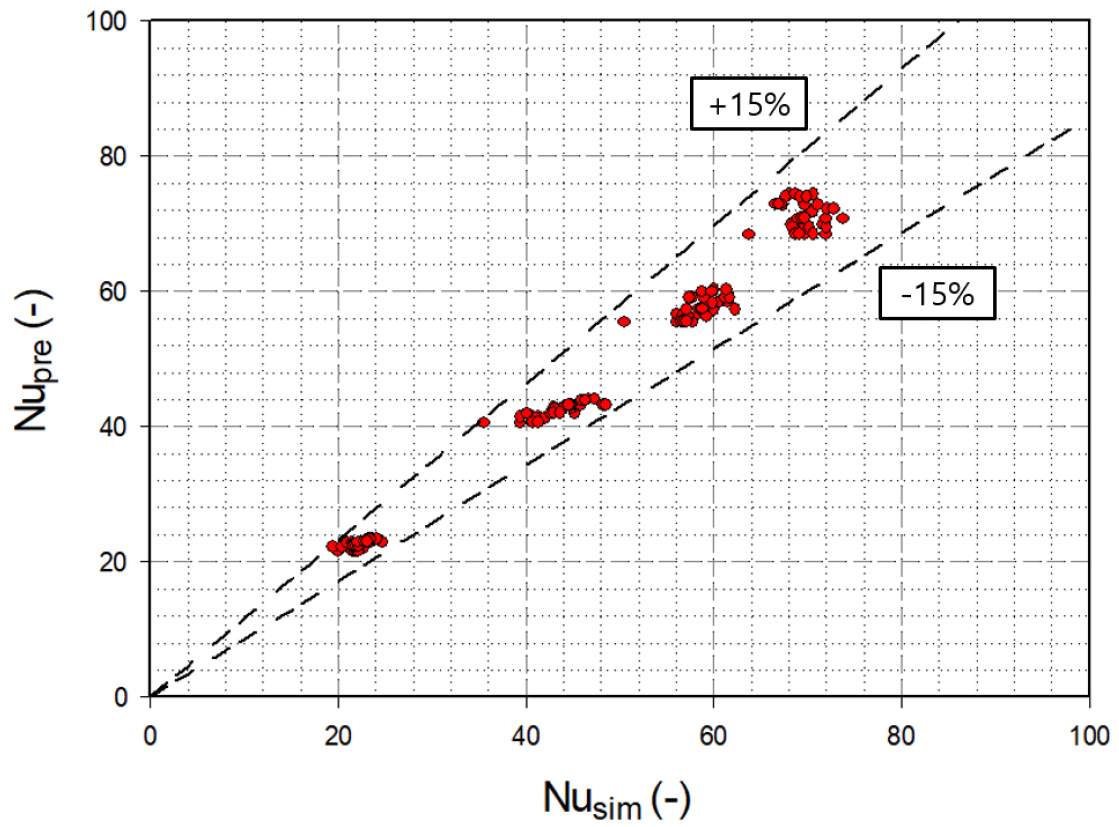
Fig. 13은 난류 촉진제 상관관계식 식(24)로 부터 얻어진 Nu 예상값인 Nupre와 CFD 시뮬레이션 Nu 수 결과값인 Nusim을 비교한 오차율을 나타낸다. Nupre와 Nusim의 오차율 모두 15% 이내의 범위에 위치하며, 평균 퍼센트 오차율은 3.24%이다.
4.2 Friction factor (f)
독립변수에 따른 f의 변화를 상관관계 식으로 나타내기 위해, 독립변수(Re, e/h, p/e, w/e) 중 각각 차례로 상관관계식으로 변환하였으며, f도 Nu와 같이 위의 과정을 거쳤을 때 상관식은 다음 식(25) 과 같다.
Fig. 14는 난류 촉진제 상관관계식 식(25)로부터 얻어진 f 예측값인 fpre와 CFD 시뮬레이션 f 값인 fsim을 비교한 오차율을 나타낸다. fpre과 fsim 의 오차율 모두 15% 이내의 범위에 위치하며, 평균 퍼센트 오차율은 5.31%이다.
5. 결 론
본 연구에서는 CFD를 사용하여 태양광/열 집열기 내 비균일 삼각 단면을 갖는 난류 촉진제의 열전달 성능 및 압력강하를 평가하였으며, 유동 조건 및 형상조건에 따른 상관관계식을 도출하는 것을 목표로 하였으며, 그 결론은 다음과 같다.
(1) 열전달 성능은 Re = 3000, e/h = 0.16, p/e = 6, w/e = 5인 조건에서 Nu = 24.73이였으며, Nus에 비해 2.03배로 가장 높게 증가하였다. 형상조건에 따라 Nu/Nus은 1.28 ~ 2.03 값을 보였다. 공기 유속이 증가함에 따라 Nu 또한 선형적으로 증가하였으며, 이는 유속이 증가함에 따라 대류 열전달 계수가 증가하였기 때문이다.
(2)압력강하는 Re = 18000, e/h = 0.04, p/e = 20, w/e = 2인 조건에서 가작 작은 f = 0.0166였으며, fs보다 2.43배 증가한 값이다. 형상조건에 따라 f/fs은 2.41 ~ 4.68 값을 보였다. e/h가 증가할수록 높은 경향을 보였으며, 이는 e/h의 증가로 마찰계수 또한 증가하며, 공기 유동 저항 면적이 증가 되었기 때문이다.
(3) 열전달 성능 변화와 압력강하 변화를 동시에 고려한 열전달 성능계수는 Re = 3000, e/h = 0.04, p/e = 10, w/e = 1인 조건에서 가장 큰 THPP = 1.22 값을 보였다. 열전달 성능 및 압력강하와는 다르게 e/h에 대한 변화는 적었으며, p/e가 낮을수록 THPP가 증가하는 것을 확인하였다.
(4) Nupre와 Nusim 및 fpre 와 fsim를 비교하였을 때, 오차율이 모두 15% 이내의 범위에 위치하며, 평균 퍼센트 오차율은 각각 3.24%, 5.31%로 신뢰할만한 상관관계식을 제시하였다.
향후 연구에서는 이 상관관계식을 이용하여 최적 성능을 가지는 난류 촉진제를 제작하여, 최적 난류 촉진제가 부착된 태양광/열 집열기의 실제 실험 성능을 평가하려 한다.