1. 서 론
2. 부유식 해상태양광 계류시스템 설계 및 안전성 평가
2.1 수중부력체 기반 계류시스템 설계
2.2 계류시스템 복원력 산정
3. 해상태양광 부유체 설계 및 수치해석
3.1 설계하중 산정 및 평가
3.2 부유체 동역학 해석 및 응답평가
4. 결 론
기호 및 약어 설명
: 파고
: 기움각
: 하중
: 변위
: 계류선 초기각도
: 선 계류선 변화 각도
: 계류선의 변화 길이
: 계류선 변화 각도
: 계류선의 장력
: 계류선의 초기장력
: 파랑 주기
: 최대 파고 높이
: 유의 파고
: 형상파라미터
: 파랑의 입사각
: 수심
1. 서 론
최근 화석연료 고갈 및 여러 가지 환경오염 방지를 위한 친환경, 신재생에너지 발전에 관한 연구가 크게 증가하고 있다. 또한, 최근 핵심기술의 발전과 공공 및 민간 부문 투자가 늘고 있어 청정에너지 자원개발이 가속화되고 있다. 그중에서 태양광 발전은 에너지 전환에서 중추적인 역할을 할 것으로 기대되나 대규모 시설을 갖추기 위해서는 넓은 영역의 대지가 필요하다. 따라서, 이러한 공간제약에 대처하기 위하여 새로운 기술과 대체 설치 장소의 요구가 커지고 있다. 최근 저수지나 연못, 방파제 등 기존의 육상지역을 벗어나서 환경적 제약이 적고 발전량을 극대화할 수 있는 설치지역으로 이동하고 있다. 육상에서 수상(내수면)으로의 에너지 생산 전환은 공간제약에 대한 문제를 해소하고 농업과의 토지 사용 충돌을 줄일 수 있으며, 환경 보호에 기여할 수 있다. 그러나, 수상(내수면) 역시 육지 내 한정적 영역으로써 공간제약 문제의 완전한 해소가 어렵기 때문에 최근 해상으로의 진출이 적극적으로 추진되고 있다. 해상에서의 에너지 생산에 관한 연구는 고정식 및 부유식 해상풍력, 부유식 진자형 또는 가동물체형 파력발전, 부유식 해상태양광발전 등 에너지 발전원뿐만 아니라 다양한 형식에 대하여 진행되고 있다. 이 중에서도 단위면적당 발전효율과 발전잠재량이 큰 해상태양광발전은 해상에 띄워지는 부유식 형태를 갖으며, 여러 개의 부유식 모듈이 모여 하나의 시스템으로 구성되는 형식이 가장 많이 활용된다. 각각의 모듈은 여러 개의 수중부력체와 이와 연결되는 구조부재, 태양광 패널이 설치되는 상부 지지구조물, 부유체의 위치를 유지하는 역할인 계류시스템으로 구성이 되며 반복적인 하중이 발생하는 해상환경과 발전시스템 운용기간을 고려할 때, 피로수명의 확보가 매우 중요하며 부유체의 운동안정성, 구조부재의 안전성 확보를 위한 핵심적인 설계기술이 요구된다. 하지만 이러한 새로운 형식의 부유식 해상태양광발전시스템은 DNV, LR, BV 등 유수의 국제 선급사들이 제시하고 있는 설계가이드라인에서 모두 지원하고 있지 못하고 있다. 따라서, 새로운 부유식 해상태양광발전시스템 구조물에 관한 물리모델을 구축하고 운동을 모사할 수 있는 지배방정식을 세워서 수치해석을 수행하여야 한다. 해상환경은 거친 파랑, 바람, 조류 등 해양환경하중의 영향으로 구조부재는 육상, 수상보다 훨씬 강한 강도와 안전성을 확보하여야 하나 구조부재의 강도의 증가를 위해서는 크기와 중량의 증가가 필연적이다. 하지만 이러한 구조부재의 크기와 중량증가는 시스템의 경제성을 떨어뜨릴 수 있으므로 구조물의 안전성과 경제성을 동시에 확보할 수 있는 최적화된 단면형상 설계가 요구된다. 유한요소법과 반응표면법을 이용한 대면적 양면형 태양광 모듈의 프레임모듈에 관한 최적설계를 통해 태양광 패널의 안전지지를 확보하고자 하는 연구가 수행되었다1). 이러한 해상태양광 부유식 구조물의 파랑하중을 저감시키고, 다양한 형태의 상호작용에 관해 연구가 진행되어 왔다2). 그리고, 부유식 및 수중 방파제를 이용한 소파성능개선에 관한 개념연구가 수행되었다3). 또한 다양한 형태의 부유식 방파제와 부유식 구조물의 상호작용을 고려한 연구를 수행한 바 있다4). 해상태양광 부유식 구조물과 같은 단위부유체가 연결된 모듈형태의 형식연구가 진행된 바 있다5). 또한, 이러한 모듈식 부유체에 관한 구조응답을 예측하고 실험을 통해 검증한 연구도 진행되어 오고 있다6). 부유체 구조물의 운동 및 구조에 관한 수치해석결과는 국제선급 DNV 가이드라인(2021)7,8,9)에 제시된 기준들을 만족하는지 검토하였다.
본 연구에서는 Glass Fiber Reinforced Plastic (GFRP) 구조부재를 갖는 부유식 해상태양광 구조물, 계류시스템에 대하여 독자적인 설계를 수행하였고, 시스템에 지배적으로 작용하는 파랑하중의 산정과 평가를 통하여 부유체의 위치유지 안정성, 구조부재의 안전을 확보하고자 하였다. 다수 부력체로 구성된 해상태양광 구조물의 부력체 및 부유체, 계류선에 작용하는 파랑하중과 운동특성은 고차경계요소법(Higher-Order Boundary Element Method, HOBEM)을 적용하여 해석 및 평가를 수행하였으며 도출된 결과를 기반으로 유한요소법(Finite Element Method, FEM)을 통하여 구조부재의 구조응답특성을 평가하였다.
2. 부유식 해상태양광 계류시스템 설계 및 안전성 평가
2.1 수중부력체 기반 계류시스템 설계
본 연구의 대상인 해상태양광 시스템의 위치유지 및 운동안전성 확보를 위하여 설치대상인 새만금 해상에서의 만조 및 간조 조건에 따라 약 7 m까지 변화하는 조위차를 고려하여 계류시스템 설계를 수행하였다. 제안된 해상태양광 계류시스템은 계류선에 수중부력체를 부착하여 수심 변화에 따라 요구되는 부유식 해상태양광 구조물의 계류 복원력을 확보하는 방식으로 그 형태는 Fig. 1, Fig. 2 및 Fig. 3과 같다.
2.2 계류시스템 복원력 산정
본 연구에서 제안된 수중부력체를 활용한 계류시스템을 고려한 해석을 수행하기 위해서 아래와 같은 비선형 방정식 형태의 복원력 곡선식을 유도하였다. 계류선이 기울어짐()에 따라 발생하는 하중() 및 변위()를 식(1)과 (2)로 나타낼 수 있으며, 식(2)로부터 기울어짐 각도()를 변위와 길이에 대한 식으로 나타낼 수 있다(식(3)). 식(1)에서 은 계류선의 수를 나타낸다. 계류선은 부유체를 본래의 위치로 유지시켜주는 역할을 하게 되는데 이를 복원력으로 나타내며 그 크기에 따라 계류선의 제원을 결정하야 한다. 계류시스템의 운동에 의해 발생하는 수중부력체에 부착된 계류선의 변화된 길이()는 식(4)와 같으며, 수중부력체와 초기 계류선 위치와의 거리가 일정함을 통해 식(5)를 구할 수 있다. 식(5)로부터 수중부력체 부착 계류선의 각도()를 초기 각도() 및 길이()에 관한 식으로 나타낼 수 있다. Fig. 4는 본 연구에서 유도한 계류선 복원력 산정에 관한 역학적 상호관계를 도식화하여 보여주고 있다.
수중부력체의 수직방향 하중은 식(7)과 같으며, 장력() 및 부착 계류선의 각도()의 변화에 관계없이 일정한 값을 가진다. 이를 통해 변화하는 장력()을 초기 장력() 및 각도()에 의한 식으로 나타낼 수 있다(식(8)).
위 식에서 구한 관계식들을 초기 하중에 대한 식(1)에 대입함으로 다음과 같은 비선형 방정식 형태의 복원력을 구할 수 있다.
식(9)로부터 설계하중()에 대한 부유식 해상태양광 구조물의 횡방향 변위를 구할 수 있으며, 식(3), (4), (6), (8)을 통해 설계하중 대비 계류삭 장력()을 산출 할 수 있다. 계류시스템 기울어짐의 변화를 나타내는 각도인 의 크기가 작을 때, , 이므로 식(1)과 (2)를 통해 선형 방정식 형태의 계류 복원력, 를 도출할 수 있다.
앞선 식으로부터 도출한 해상태양광 계류시스템의 계류복원력 곡선은 Fig. 5와 같다. 결과에서 알 수 있듯이 만조 시 계류선 변위는 약 3.5 m 이내, 간조 시 10 m 발생할 수 있으며, 이때의 계류선의 장력은 14톤 ~ 18톤까지 발생하므로 Mooring Breaking Limit (MBL)을 견딜 수 있는 계류선을 결정해야 한다. 따라서, 간조 시 부유체의 복원시간은 만조 시 보다 다소 많이 소요될 것으로 예상된다.
3. 해상태양광 부유체 설계 및 수치해석
3.1 설계하중 산정 및 평가
본 연구의 대상인 해상태양광 시스템의 구조부재는 최소요구 단면력을 산정하여 부재배치 설계와 초기치수 결정을 수행하였고, 해상상태 운용 시 부유체 운동성능에 관한 수치해석을 통해 설계검토를 수행하였다. 해양구조물의 건전성 판정을 위해서는 먼저 설계된 구조물의 제원을 통해 파랑, 바람, 조류하중 등을 평가의 수행이 요구된다. 하중평가를 위한 해상태양광 시스템 및 수치해석 영역은 Fig. 6과 같으며, 해석 영역 구조물의 크기는 길이 25.2 m, 폭 21.2 m이다. 선박해양플랜트연구소(KRISO)에서 개발한 부유체와 파랑에 관한 지배방정식을 정식화를 통해 수치코드를 구축하였고 경계요소법 및 유한요소 영역을 설정하여 수치해석을 수행하였다. 이때, 파랑유동의 포텐셜 및 연결체 응답은 각각 경계요소(Boundary element) 및 유한요소(Finite Element) 영역으로 한 경계면에 관하여 그린함수를 통해 정리하여 이산선형방정식 형태로 표현할 수 있으며 Convolution integral을 통해 시간영역으로 변환하여 비주기 하중형식의 적용 및 2차 표류력(drift)의 계산이 가능하다. 한편 풍하중, 조류하중은 모리슨 식으로 산출하였다.
(1) 파랑하중 산정 및 평가
부유식 해상태양광 구조물에 작용하는 설계하중 중 파랑하중 및 표류력은 유동해석 수치해석 기법의 일종인 고차경계요소법(Higher-Order Boundary Element Method, HOBEM)을 통해 산정하였다. 고차경계요소법(HOBEM)은 기존 경계요소법(Boundary Element Method, BEM)에 고차경계요소를 적용하여 수렴성과 정확성을 향상시킨 방법으로, 이에 대한 자세한 설명은 참고문헌(Choi et al., 2001; Hong et al., 2005)을 통해 확인할 수 있다10,11). 고차경계요소법 적용을 위한 수치모델은 Fig. 7과 같이 보여주고 있고, 2080 절점 및 480 요소로 구성된다. 해상태양광 부유체 구조물의 파랑하중 해석을 위한 설계파 및 해석 조건은 Table 1과 같다.
Table 1
Design wave and analysis condition for wave loads evaluation
위 해상상태조건으로 수치해석을 통해 얻은 파랑하중 평가결과가 Figs. 8, 9, 10, 11에 제시되어 있다. Figs. 8과 9는 만조조건 시 부유체에 작용하는 파랑하중의 시계열을 파향 0, 45, 90도에 대해 제시한 것으로서 Fig. 8은 규칙파 시, Fig. 9는 불규칙파 시 결과를 각각 나타내고 있다. Figs. 10과 11은 간조조건 시 부유체에 작용하는 파랑하중의 시계열로서 각각 규칙파, 불규칙파 중 결과를 나타내고 있다.
파향 0도에서 최대파랑하중은 만조조건에서 규칙파 및 불규칙파 시 각각 0.097톤, 1.476톤이었으며 간조조건에서 0.081톤, 1.468톤이었다. 파향 45도에서 최대파랑하중은 만조조건에서 규칙파 및 불규칙파 각각 0.721톤, 0.782톤이었으며 간조조건에서 0.711톤, 0.772톤 이었다. 또한, 파향 90도에서는 최대 파랑하중은 만조조건에서 규칙파 및 불규칙파 각각 0.388톤, 3.348톤이었으며 간조조건에서 0.366톤, 3.353톤으로 산정되었다. 파랑하중의 경우 규칙파로 가정하여 응답을 계산하여 그 크기를 예상하고, 실제 설치되는 대상해역의 해상환경정보를 통해 실제 환경에 맞도록 불규칙파를 시간영역으로 생성하게 된다. 따라서, 불규칙파 응답결과는 일반적으로 규칙파보다 매우 클 때도 있고, 작은 크기가 연속될 때도 있다. 예측하지 못한 영역에서 큰 응답들을 분석해 내고, 그 영향이 얼마나 되는지 파악해야 하는데 본 수치해석 결과는 약 15배 정도 큰 것을 알 수 있었다. 이는 새만금지역의 해상상태와 수심을 고려하여 보았을 때 파랑하중의 크기가 작지 않음을 의미한다. 만조와 간조의 차이가 크지 않아서 가변수심의 영향은 크게 고려하지 않아도 되는 것으로 분석된다. 다만, 계류시스템 설계 시 만조와 간조차이를 고려한 계류선의 설계가 필요하며, 수심이 변하더라도 해상태양광 부유체 구조물의 응답변화에는 큰 영향이 없도록 계류선의 배치설계가 매우 중요하다. 한편 파랑하중의 2차 성분에 의한 표류력 또한 고차경계요소법으로 산출하였고 해석결과, 파향 0도에서 표류력은 만조 및 간조조건에서 각각 1.932E-06톤, 1.669E-06톤이었으며 파향 45도에서 각각 8.838E-06톤, 8.830E-06톤으로 나타났다. 파향 90도의 결과는 각각 1.931E-06톤, 1.760E-06톤의 결과를 얻었다. 본 구조물의 경우 2차 표류력은 앞 절에서 제시한 파랑하중에 비해 미미함을 알 수 있다.
(2) 풍하중 산정 및 평가
해석 영역의 부유식 해상태양광 구조물에 작용하는 설계하중 중 풍하중은 아래 식과 같이 계산할 수 있다.
이 때 위 식에서의 각 변수항목이 나타내는 의미와 계산 값은 Table 2와 같다. 설계풍속 50 m/s 시 총 풍하중은 4.72 tonf가 발생하였다.
Table 2
Result of wind loads analysis for GFRP floating photovoltaic structure
(3) 조류하중 산정 및 평가
해석 영역의 부유식 해상태양광 구조물에 작용하는 설계하중 중 풍하중은 아래 식과 같이 모리슨 형태로 계산할 수 있다.
이 때 위 식에서의 각 변수항목이 나타내는 의미와 계산 값은 Table 3과 같다. 설계조류속 0.8 m/s 시 총 조류하중은 1.107 tonf가 발생하였다.
Table 3
Result of current loads analysis for GFRP floating photovoltaic structure
| Item | Symbol | Calculated value | Remark |
| Drag coefficient | 2.0 |
Theoretical maximum value (Ministry of Ocean & Fisheries, 2017)12) | |
| Water density | 1,025 [kg/m3] | Sea water | |
| Current velocity | 0.8 [m/s] | Designer’s criterion | |
| Projected area | 0.259 [m2] | Calculated from drawings | |
| Total buoyancy module | 65 | ||
| Current loads | 1,107 [tonf] | Equation (2) |
이상 검토된 파랑, 바람, 조류 등의 설계하중 각 항목에 관한 총 하중에 관한 사항은 Table 4에 요약하였다.
Table 4
Summary of design forces
앞 절에서 계산한 계류복원력 곡선(Fig. 5)으로부터 설계하중 조건에 대한 해상태양광 부유체 구조물의 횡방향 변위와 계류삭 장력을 산출할 수 있으며, 그 결과는 만조조건에서 총 설계하중 9.175톤, 횡방향 변위 3.133 m, 계류선 장력 7.411톤이었으며, 간조조건에서 총 설계하중 9.180톤, 횡방향 변위 7.2 m, 계류선의 장력이 2.369톤으로 산정되었다. 이로써, 설계하중은 계류선 만조조건에서의 최대장력치인 7.411톤 이상의 허용장력을 갖는 계류시스템으로 선정해야함을 알 수 있었다.
3.2 부유체 동역학 해석 및 응답평가
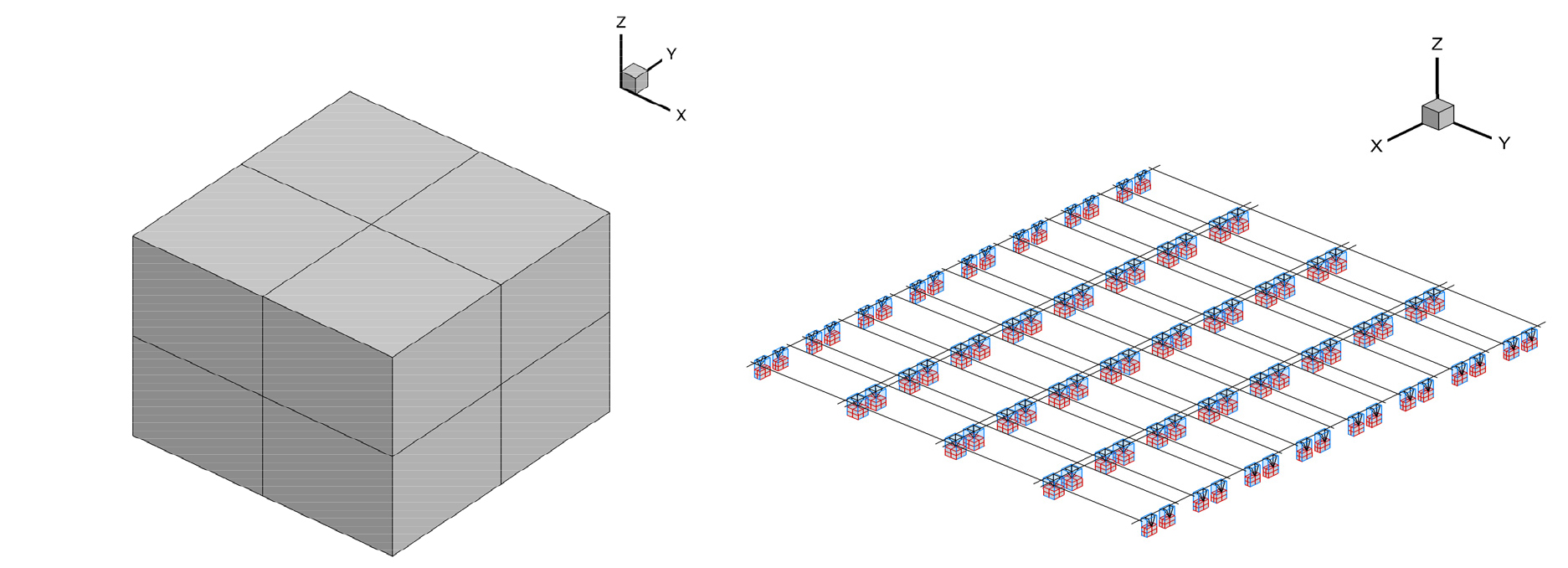
본 연구의 수치해석 영역의 구조물은 4개의 모듈로 구성되며, 각 모듈은 16개의 부력체와 각 부력체를 연결하는 GFRP 연결체로 구성된다. 각 모듈은 폴리우레탄 연결봉을 통해 연결되며, 본 해석에서는 GFRP와 동일한 강성으로 가정하여 해석을 수행하였다. 부력체, 연결체 및 단위 모듈의 물성치를 Table 5에 정리하였다. 해석영역 해상태양광 부유체 구조물의 유동해석을 위한 유동 및 구조 각각의 수치해석 모델은 Fig. 12와 같다. 앞 절에서 언급한 바와 같이 유체영역은 고차경계요소, 구조영역은 유한요소로 해석을 수행하였다. 고차경계요소로 모델링된 부력체 및 보 요소로 모델링된 연결체를 포함하는 해석 영역의 해상태양광 수치모델링하였고, 부력체의 경우 2080개의 절점, 480개의 고차 패널요소로 구성되며, 연결체는 1088의 절점, 1504개의 보요소가 사용되었다.
Table 5
Material properties of floating offshore photovoltaic system (FOPS)
해상태양광 구조물에 대하여 해석조건인 규칙파 조건(H = 3 m, T = 4.0 sec.)에서의 구조물에 작용하는 파랑하중 분포는 Fig. 13과 같다. 만조(수심 20 m)/간조(수심 13 m) 조건에 대하여 각각 해석을 수행하였으며, 파랑하중 분포 결과에 대해서는 큰 차이가 발생하지 않았음을 확인할 수 있었다.
해상태양광 부유체 구조물의 파랑 중 구조안전성 평가를 위한 구조해석 결과는 Fig. 14와 같으며 구조물의 변형 형상 및 굽힘/전단 응력의 시계열 결과를 보여주고 있다. 또한, Fig. 15는 해상태양광 부유체 구조물 연결체에 작용하는 주요 굽힘응력의 시계열 구조응답을 보여주고 있다.
각 파랑하중 조건에 따른 구조응답을 분석한 결과, 수심에 의한 구조응답 결과의 차이가 거의 없음을 확인할 수 있으며, 최대응력의 경우, 불규칙파 조건에서 발생함을 확인할 수 있었다. 계류시스템에 의해 발생하는 계류하중에 의한 구조응답을 평가하기 위한 정적 구조해석을 수행하였고 실제 해상태양광 계류시스템의 경우, 수선면 근처에 계류용 균형 부력체가 있으나, 본 해석에서는 균형 부력체와 가장 가까운 상부구조물 지지용 부력체에 계류하중이 작용하도록 하였다. 수치해석을 통해 계산된 최종 계산된 굽힘응력에 관한 결과는 Table 6과 같이 정리하였다. 총하중을 고려하였을 경우, 설계단면의 크기를 대폭 증가시키고 구조적인 보강을 수행할 필요가 있으며, 또한 파랑하중의 저감을 위해 해양 표면(splash zone)에서의 단면적을 최소화해야 함을 알 수 있었다.
Table 6
Material properties of floating offshore photovoltaic system (FOPS)
4. 결 론
본 연구에서는 GFRP (Glass Fiber Reinforced Plastic) 구조부재를 갖는 부유식 해상태양광 구조물, 계류시스템에 관한 독자적인 설계를 수행하였고, 시스템에 지배적으로 작용하는 파랑하중산정과 평가를 통해 부유체의 위치유지 안정성, 구조부재의 안전을 확보하고자 하였다. 다수 부력체로 구성된 해상태양광 구조물은 부력체 및 부유체, 계류선에 작용하는 파랑하중 및 운동특성은 고차경계요소법(Higher-Order Boundary Element Method, HOBEM)으로 유체동역학해석을 통하여 산정 및 평가를 수행하였다. 유체동역학해석을 통해 계산된 파랑하중 및 운동특성을 적용하여 유한요소법(Finite Element Method, FEM)을 통하여 구조부재의 구조응답특성을 평가하였다. 이를 통해 얻은 결과는 다음과 같다. GFRP 재료의 경우, 굽힘에 대한 허용응력의 크기는 GFRP의 항복강도를 고려하여 볼 때, 매우 높은 대역의 재질을 채택해야 함을 알 수 있었다. 만조와 간조 조건에 따라 규칙파와 불규칙파의 응답결과를 살펴보면, 새만금지역의 해상상태와 수심 보았을 때 파랑하중의 크기가 작지 않음을 의미한다. 또한, 만조와 간조의 차이가 크지 않아서 가변수심의 영향은 크게 고려하지 않아도 되는 것으로 분석되었고, 표류력의 경우 파랑하중에 비해 미미하였다. 다만, 계류시스템 설계 시 만조와 간조차이를 고려한 계류선의 설계가 필요하며, 수심이 변하더라도 해상태양광 부유체 구조물의 응답변화에는 큰 영향이 없도록 계류선의 배치설계가 매우 중요함을 알 수 있었다. 계류하중의 경우, 집중하중으로 작용함에 따라 매우 큰 응력이 작용함을 확인할 수 있었는데, 향후 설치조건 및 해양환경조건(최대파고, 풍속, 조류 등)에 맞도록 적정한 단면과 기준강도의 영역을 제안할 필요가 있다. 본 연구에서의 계류선 배치 특성으로 인하여 계류하중이 하나의 부유체에 집중되어 국부적으로 응력이 집중 분포되는 경향이 발생되는데 이는 추후 계류력을 분산시키거나 감소시킬 수 있도록 충분한 개선방법이 제시되어야 하며 계류방법을 변경할 경우 GFRP 부재의 응력을 재평가하게 된다. 본 연구에서 제시한 전체적인 설계순환(design spiral)은 기존의 전통적인 해양부유구조물이 아닌 이렇게 모듈형태의 새로운 형식의 부유식 구조물 설계에 유용하게 활용될 수 있을 것으로 판단된다. 또한, 설계기법과 절차는 이와 유사한 해상태양광 부유구조물에 적용될 수 있도록 일반화가 가능할 것으로 판단된다. 안전성과 경제성을 고려하여 최적화된 단면형상 설계가 요구되며 이는 향후 연구로써 진행할 예정이다.