1. 서 론
2. 아크 검출 과정
3. 대역 통과 필터 설계
4. 주파수 분석 방법
4.1 Fast Fourier Transform (FFT)
4.2 Discrete Wavelet Transform (DWT)
4.3 에너지 계산(Parseval theorem)
5. MATLAB 시뮬레이션
5.1 FFT 기법
5.2 DWT 기법
6. 실험 및 검증
7. 결 론
1. 서 론
환경 및 에너지 정책에 따라 태양광 발전설비는 지속적으로 증대되고 있으나 PV 시스템은 다양한 환경 조건에 노출됨으로 인해 태양광 시스템 내부에서 발생하는 문제 또는 고장이 발생할 수 있다. 이러한 문제 중 DC 아크는 PV 시스템의 안정성과 성능에 큰 영향을 끼친다. 아크는 직렬 아크와 병렬 아크로 구분할 수 있는데 병렬 아크의 경우는 두 지점 간의 전압차가 커서 고장 전류가 크기에 기존의 차단기로도 차단이 가능하다. 병렬 아크가 발생했을 경우 고장 발생점의 임피던스가 낮아지게 되고 최종적으로 단락이나 지락으로 이어져 사고가 발생한다. 직렬 아크는 부하와 전기적으로 직렬 연결되어 있는 부분에서 발생하는데, 이때 흐르는 아크전류는 아크 발생 시의 임피던스에 의해 제한되어 에너지 레벨이 낮기 때문에 기존 차단기의 보호 레벨 범위에 속하지 않는다. 특히 일부 비선형적 특징을 가지는 위상제어부하에서는 아크가 발생하지 않은 정상상태에서도 아크신호와 유사한 고주파 신호가 발생하기 때문에 아크신호의 검출에 어려움이 있다1).
PV 시스템에서의 DC 직렬 아크 검출 방법으로 전류의 주파수 성분을 분석하여 아크 노이즈 성분 분석을 통해 아크 발생을 판단한다. PV 패널 사이를 연결하는 커넥터의 연결부위 및 접속함에 연결된 체결 부위의 접속 불량으로 DC 직렬 아크가 발생될 때, DC 직렬 아크의 발생은 0.07초에서 형성이 되고 0.5초의 아크가 1초 이상 스파크 현상으로 지속되면 전기화재가 발생한다. 아크 감지차단기를 통해 아크 발생 시 태양광 인버터가 자동으로 전기를 차단하기 위해서는 적절한 알고리즘이 필요하다. 2016 43번째 IEEE 컨퍼런스(PVSC) 보고서는 태양광 DC 직렬 아크 전류의 고조파 변화는 거의 없으며 저주파(10 kHz 미만)에서도 크기가 작은 아크 전류 신호를 감지 가능하다고 보고했다2). 본 연구에서는 PV 시스템에서의 DC 직렬 아크의 위험성 및 아크가 전기화재로 이루어지는 시간을 고려하여 0.5초 내에 DC 직렬 아크를 빠르게 검출하는 것을 목표로 하고, 그 방법으로 낮은 샘플링 주파수 20 kHz에서 크기가 작은 DC 직렬 아크 전류의 주파수 특성을 빠르게 분석하고 식별하기 위해 최근 주파수 분석 방법 중 가장 널리 쓰이는 FFT (Fast Fourier Transform)와 DWT (Discrete Wavelet Transform) 기법을 사용하였다. 시뮬레이션으로 알고리즘을 검증한 후, UL1699B 아크 시험조건을 기반으로 실험을 진행하였다. 이때 아크 에너지는 750 J을 넘지 않으며, 2.5초 이내에 아크를 차단해야 한다. 마지막으로 두 주파수 분석 방법을 비교 분석한 후 가장 정확하며 효율적인 DC 직렬 아크를 검출하는 알고리즘을 구현하였다.
2. 아크 검출 과정
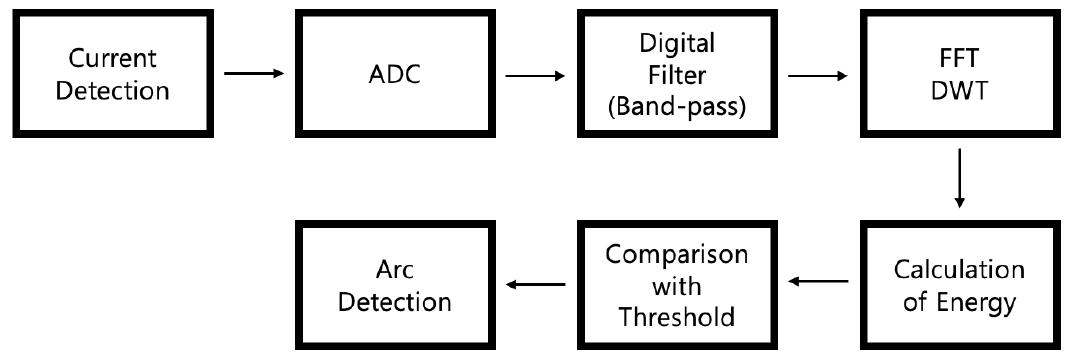
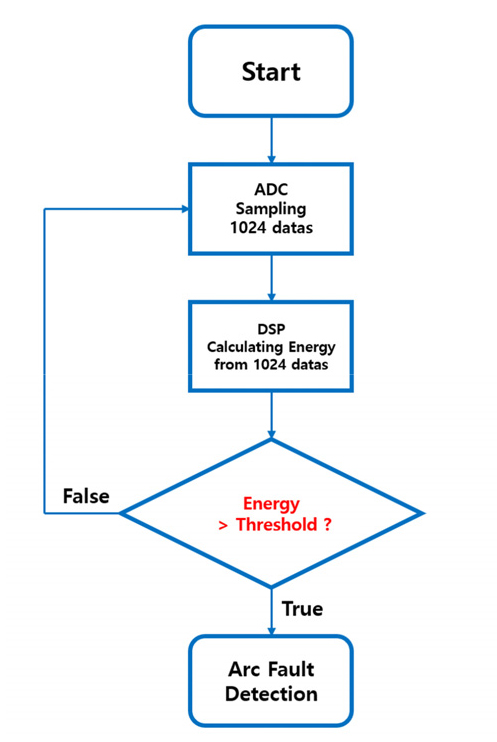
아크 노이즈는 정상적일 때 노이즈와 중첩되며 아크에 의해 생성된 노이즈는 핑크 노이즈 특성을 갖는다. 또한 0.1 kHz ~ 100 kHz의 주파수 대역은 나머지 DC 직렬 아크 검출에 유용하다. DC 직렬 아크가 존재할 때 120 Hz 인버터 노이즈 및 60 Hz 계통 노이즈가 포함되어 있기 때문에 이 주파수 대역은 아크 검출 성능 저하를 초래할 수 있다3). 따라서 적절한 대역통과필터를 설계해야 한다. DC 직렬 아크 신호의 검출 및 판단하는 과정은 Fig. 1과 같으며 다음과 같이 설명한다. 먼저 발생시킨 DC 직렬 아크 신호는 샘플링 주파수가 20 kHz인 ADC (Analog to Digital Converter)를 통해 1,024개를 측정하여 아크 특정 주파수 성분 검출을 위해 디지털 대역 통과 필터(Digital BPF)를 적용하여 노이즈 및 아크 이외의 성분을 제거한다. 디지털 대역 통과 필터의 대역폭은 Nyquist 샘플링 이론을 고려하여 2.5 ~ 15 kHz로 설정하고 디지털 대역 통과 필터를 통과한 이산 신호는 FFT 또는 DWT (mother wavelet: Daubechies 4) 기법의 MSD (Multi-level Signal Decomposition) 작업을 통하여 주파수 영역으로 변환한다. 마지막으로 특정 주기별로 주파수의 성분인 에너지를 계산한 후, 각각의 에너지 값의 임계값을 설정하여 특정 임계값을 초과할 경우 아크로 판단한다.
3. 대역 통과 필터 설계
직렬 아크 검출 방법으로는 주로 전류의 주파수 성분을 분석하여 아크 노이즈 성분 분석을 통해 아크 발생을 판단한다. 아크 잡음은 정상적일 때 잡음과 중첩되며 아크에 의해 생성된 잡음은 핑크 잡음 특성을 갖으며, 0.1 ~ 100 kHz의 주파수 대역은 나머지 현재 스펙트럼보다 직렬 아크 검출에 유용하다2). 따라서 본 프로젝트에서는 아크상태와 정상상태의 특성을 충분히 반영하는 필터를 설계하기 위해, 100 ~ 1,000 Hz 미만의 주파수는 입사 방사진동, 120 Hz 인버터 노이즈 및 60 Hz 계통 노이즈가 포함되어 있으므로 아크 검출의 성능 저하를 초래할 수 있기에, 검출 주파수 범위를 1 ~ 100 kHz 사이로 좁혔다. 더불어 실험 결과에 따르면, Table 1과 같이 필터-1 (대역통과 주파수 0 ~ 25 kHz), 필터-2 (대역통과 주파수 25 ~ 50 kHz) 구조에서 다른 필터 구조에 비하여 우수한 검출 성능을 보이는 것으로 알려져 있다4).
따라서 본 연구에서는 2.5 kHz ~ 15 kHz의 대역대의 특성을 이용하여 정상신호와 아크신호를 구분하고자 한다. 대역통과 필터를 이용해서 해당 주파수 대역의 신호는 통과시키고, 그 미만 또는 초과되는 주파수 성분을 갖는 신호를 제거하고자 4차 Butterworth 대역통과필터를 적용하였다.
Table 1
Arc detection performance according to filter types
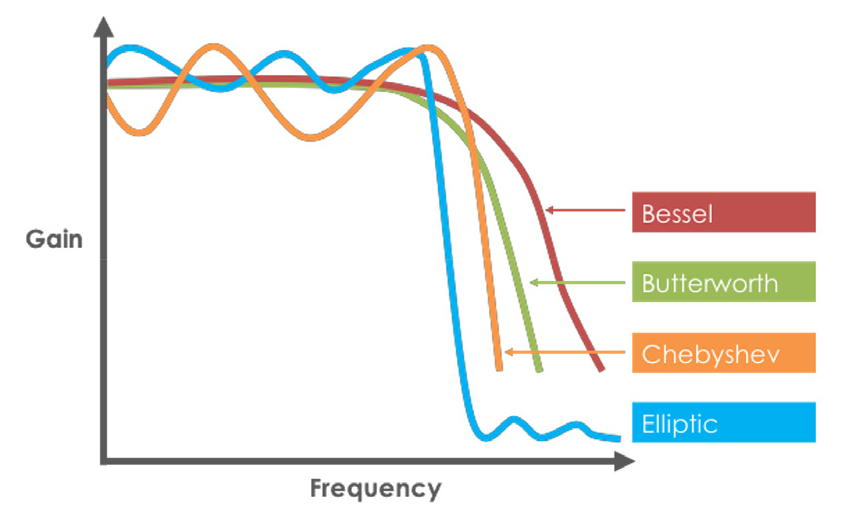
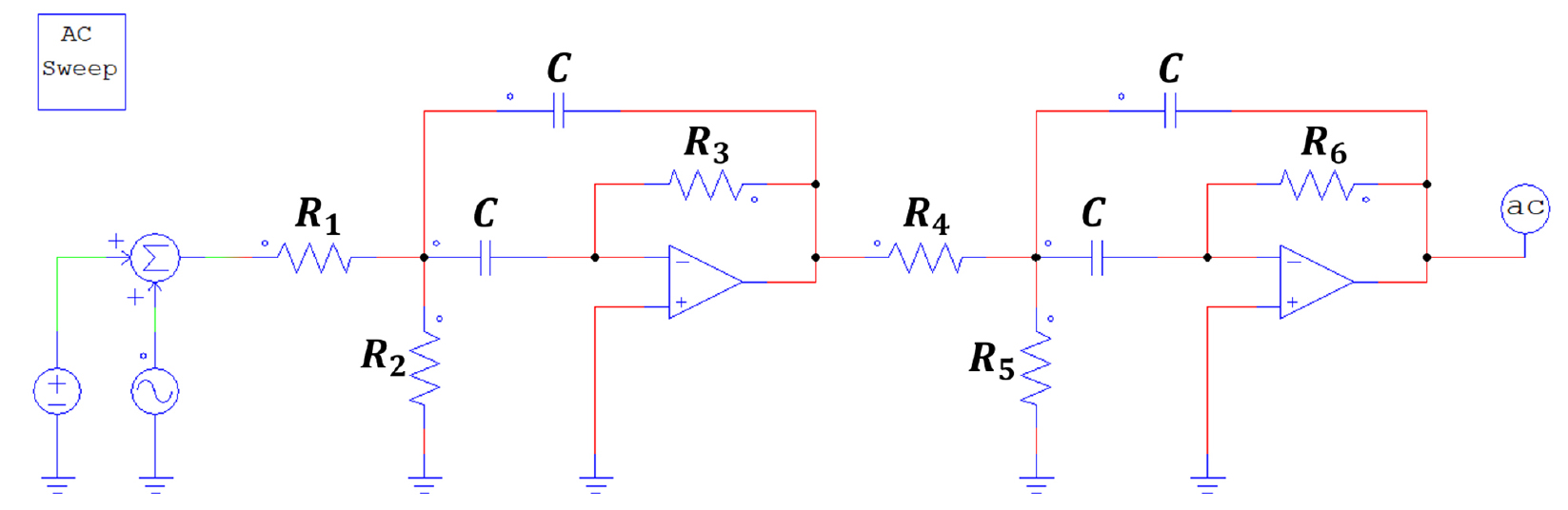
본 연구에서는 원하는 주파수 범위를 정확하게 통과시키며 신호의 왜곡을 최소화하며 정확한 아크 신호를 추출하기 위해 Butterworth 필터를 선정하였다. Fig. 2의 다양한 필터 종류 중, Butterworth 필터는 통과 대역이 평평하고 값이 떨어지는 부분(Skirt)이 다른 필터에 비해 완만한 특성을 가진다. 따라서 Butterworth 필터의 평평한 통과 대역을 통해 주파수 통과 대역을 오류 없이 전달할 수 있고, 완만하게 떨어지는 Skirt 부분을 통해 Skirt 영역의 주파수 값의 노이즈를 최소화하여 왜곡을 줄일 수 있다. 따라서 본 프로젝트에서 설계한 4차 Butterworth의 회로도는 Fig. 3과 같다.
Fig. 3과 같은 4차 Butterworth Band Pass filter (BPF)는 중심 주파수가 2.5 kHz인 2차 BPF와 중심주파수가 15 kHz인 2차 BPF를 직렬 연결하는 방식으로 구현하였다.
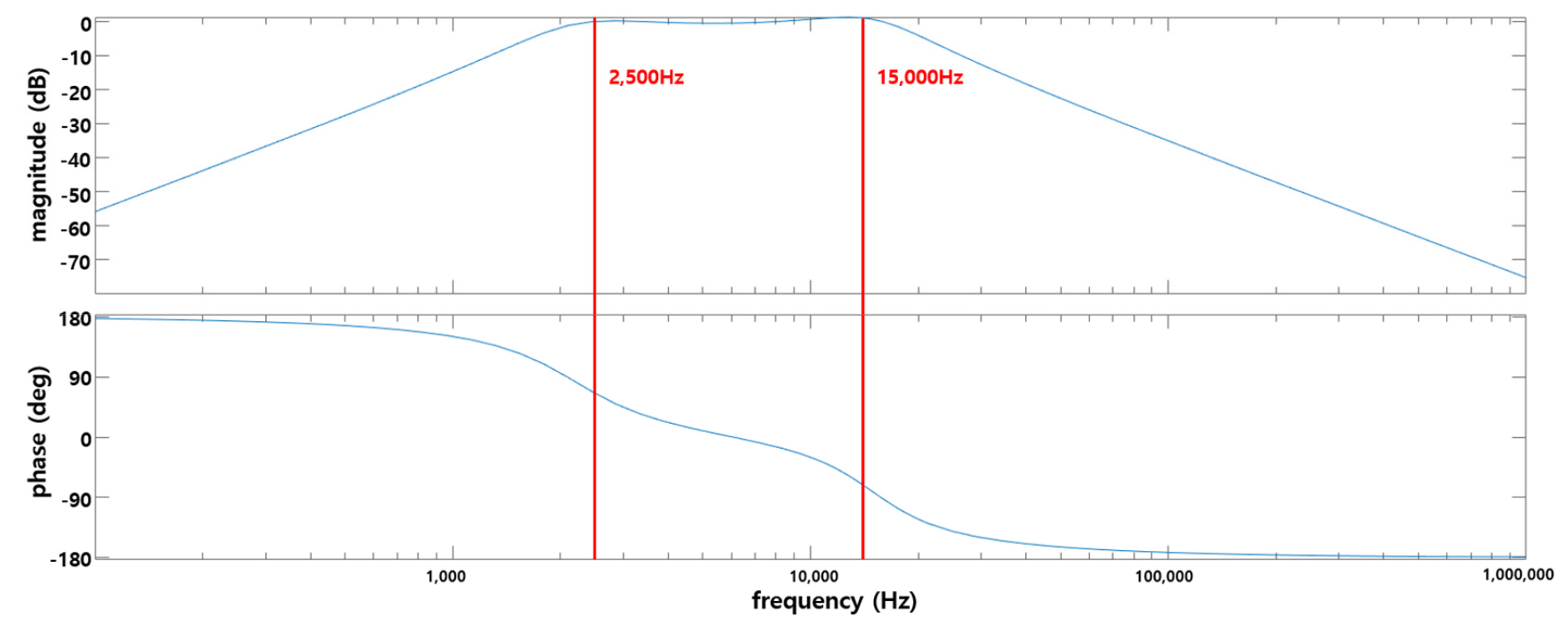
Fig. 4에서는 설계된 4차 Butterworth 대역통과필터의 주파수 응답 특성을 나타냈다. 본 연구에서는 먼저 4차 Butterworth 대역통과필터의 회로도를 설계한 후, 전달함수를 사용하여 설정한 대역통과 주파수인 약 2.5 kHz ~ 15 kHz가 나오는 것을 MATLAB을 통해 성공적으로 확인하였다. Fig. 5는 입력신호에 대역통과 필터를 적용시킨 후의 결과이다. Fig. 5에서 보는 바와 같이, 2.5 kHz ~ 15 kHz 주파수 대역에 있는 신호만 통과되고 그 이외의 주파수 성분에 대한 신호는 제거되었음을 확인할 수 있다.
디지털 필터를 설계하는 여러 가지 방법이 있지만 본 연구에서는 앞에서 기술한 바와 같이 아날로그 필터를 설계한 후 쌍선형 변환(Bilinear transformation)을 사용하였다. 쌍선형 변환은 아날로그 영역과 디지털 영역에서 전달 함수 표현을 유지해주는 변환으로서 필터 변환 기법들 중 가장 널리 사용되는 방법이다.
4. 주파수 분석 방법
4.1 Fast Fourier Transform (FFT)
이산 푸리에 변환(DFT: Discrete Fourier Transform)은 시간 영역의 연속적인 신호를 주파수 영역으로 변환하여 주파수 성분을 분석할 수 있는 알고리즘이다. 주어진 신호 에 대한 DFT는 식(1)과 같이 정의된다.
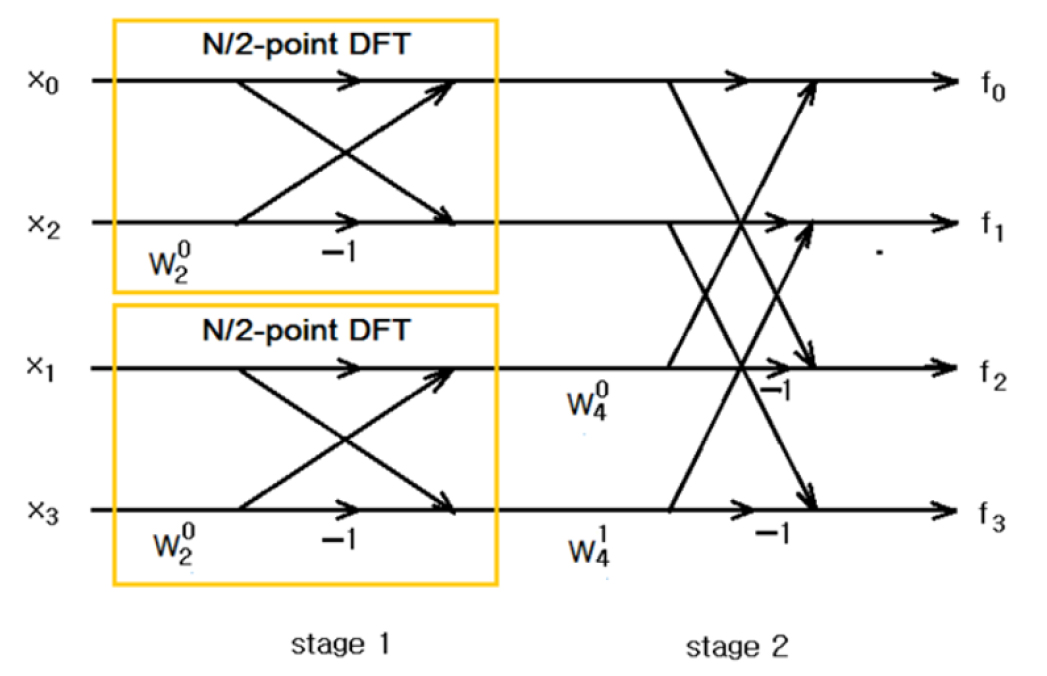
식(1)의 은 데이터의 크기이며, 는 주파수 인덱스이다. DFT는 의 계산 복잡도를 가진다. 따라서 많은 연산량이 필요한데 FFT는 Cooley-Tukey 알고리즘을 기반으로 계산 복잡도를 으로 줄인다. 이 Radix-2 FFT는 잘 알려진 알고리즘 중 하나로 입력 데이터의 크기가 2의 거듭 제곱일 때 효과적이다. 따라서 본 연구에서는 으로 한다. 일 때를 간단한 예로 들면 Radix-2 FFT 알고리즘의 핵심인 butterfly 연산은 회전인자 의 주기성을 활용해서 연산량을 줄인다.
Fig. 6을 보면 입력 데이터가 Radix-2 FFT 알고리즘을 따라 입력 데이터가 순서대로 배열되어 있지 않다. 이는 신호 수열을 계속적으로 두 개의 반쪽 수열로 나누는 과정에서 비롯된 것이다. 만일 처음 배열을 적당히 잘 재배열해 놓는다면, 그 다음부터는 보다 큰 추가 메모리 없이 전체 배열의 FFT를 완료할 수 있다. 입력 수열의 순서는 시간 변수 n을 2진수로 바꾼 뒤 비트 순서를 역으로 하여 다시 십진수로 나타낸 것과 동일하다. 이를 역 비트순(bit-reversed order)이라 한다.
4.2 Discrete Wavelet Transform (DWT)
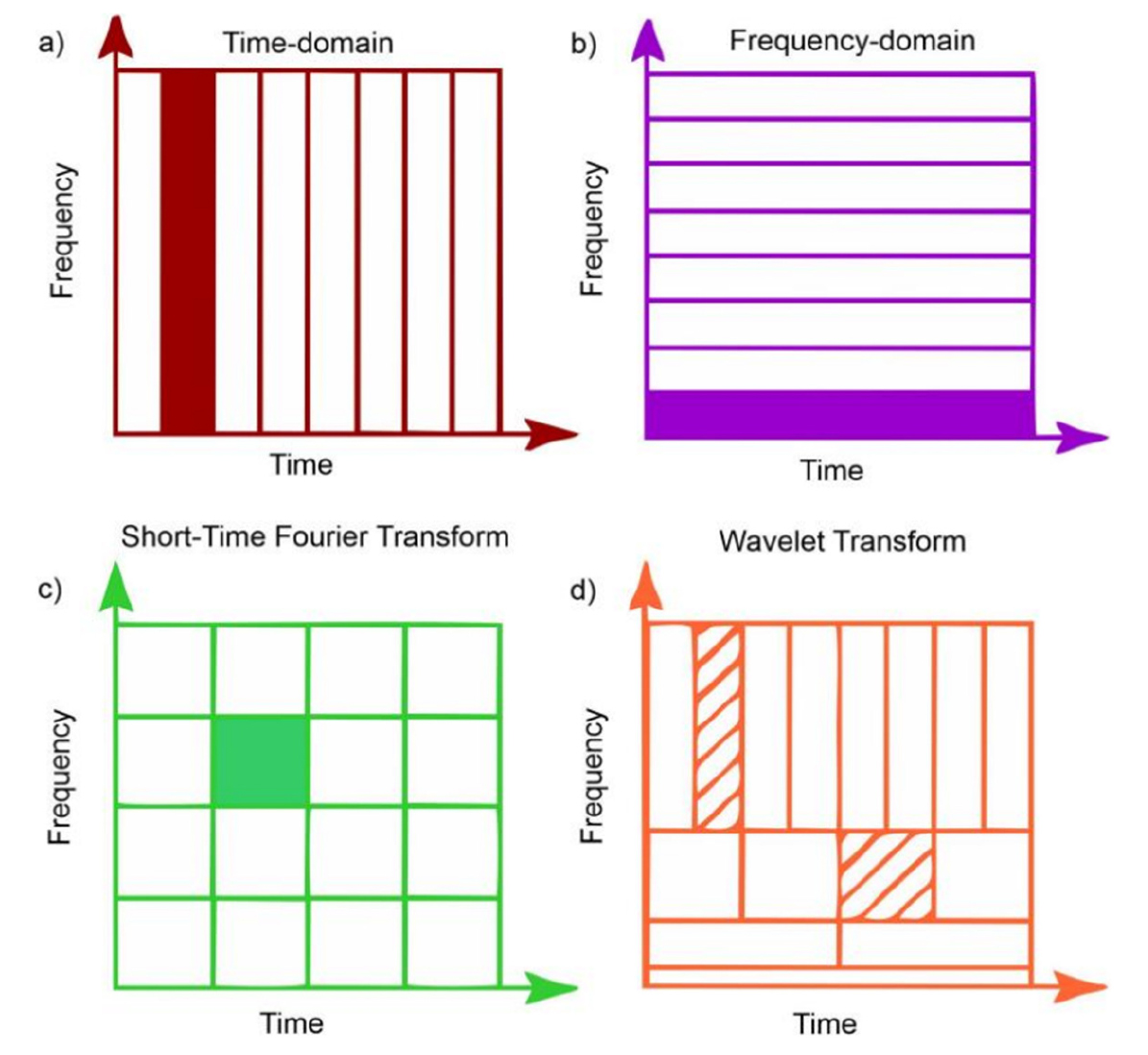
Fig. 7은 FFT, STFT, 웨이블릿 변환을 비교한 그림이다. FFT의 가장 큰 문제점은 시간영역의 정보를 완전히 잃어버린다는 것이다. 그 문제를 해결한 것이 STFT (Short-Time Fourier Transform)와 웨이블릿 변환(Wavelet Transform)이다. STFT는 슬라이딩 윈도우의 크기에 따라 주파수 영역과 시간 영역의 해상도는 서로 trade off 관계이다. 하지만 웨이블릿 변환은 주파수 크기에 따른 유연한 윈도우 크기를 설정하여 시간 영역과 주파수 영역 모두 해상도를 높게 가져갈 수 있다. 웨이블릿 변환은 CWT (Continuous Wavelet Transform)과 DWT (Discrete Wavelet Transform)가 있다. 본 연구에서는 ADC를 통과한 이산 신호를 처리하기 때문에 DWT를 사용한다. 이산 웨이블릿 변환은 mother wavelet을 이용하여 신호를 특정 주파수 대역으로 분해할 수 있다.
웨이블릿 변환은 해당 신호가 주어진 scale 과 location 변수를 가진 웨이블릿 함수와 얼마나 닮았는지에 대한 양에 해당되는 계수를 구하는 과정이다. 본 연구에서 사용된 mother wavelet인 db4 (Daubechies 4) 웨이블릿은 필터 계수가 적고 대칭 구조를 가지기 때문에 계산 효율성이 높으므로, 신호 분석 작업을 효율적으로 수행할 수 있다. 따라서 db4는 아크 검출을 빠르게 할 수 있는 계산 효율성과 정확한 계산 작업이 가능한 웨이블릿 함수이므로 아크 검출을 위한 웨이블릿 함수로 선정했다.
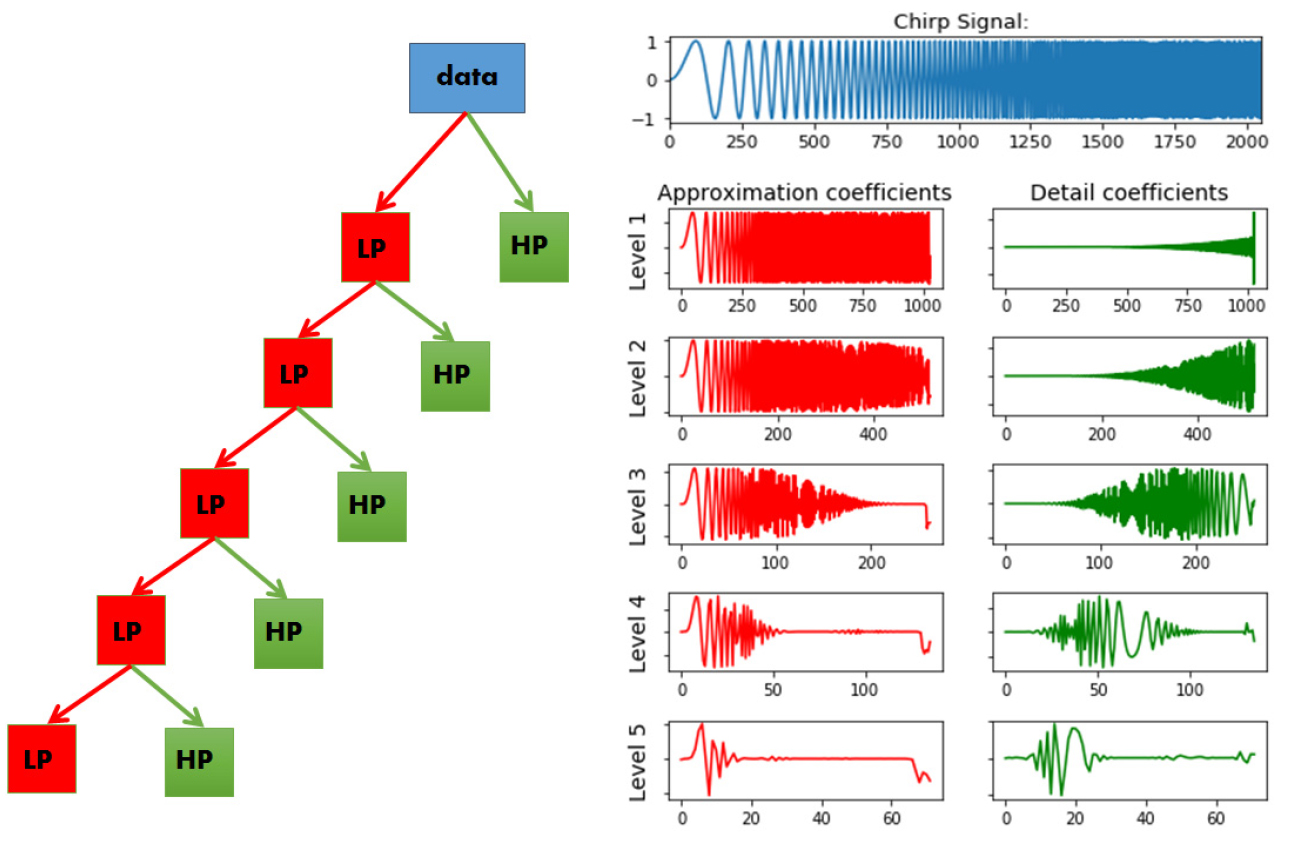
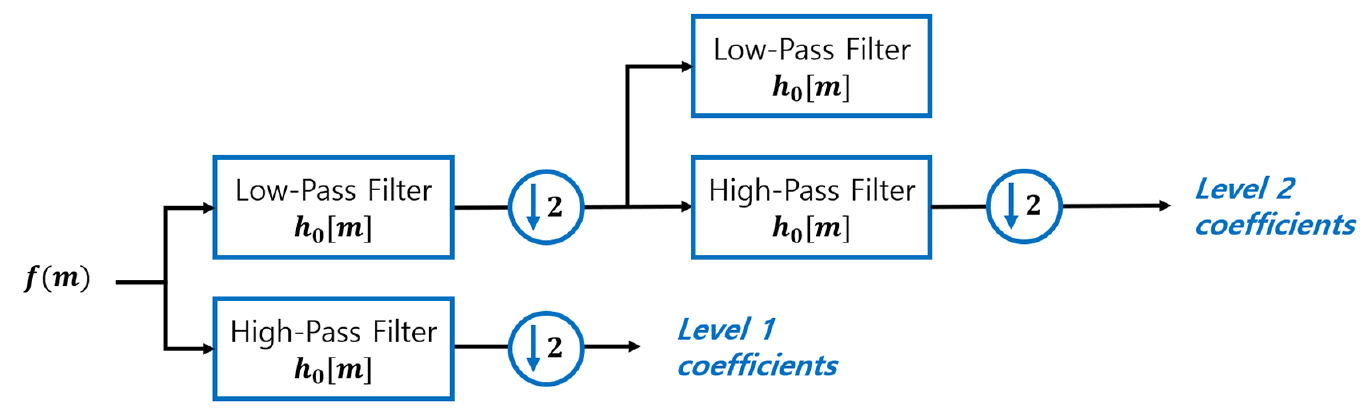
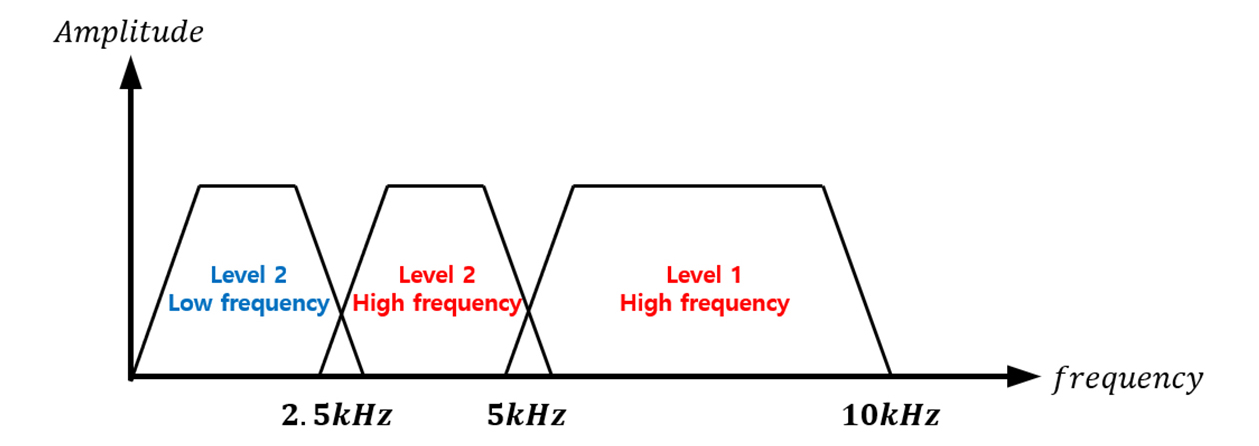
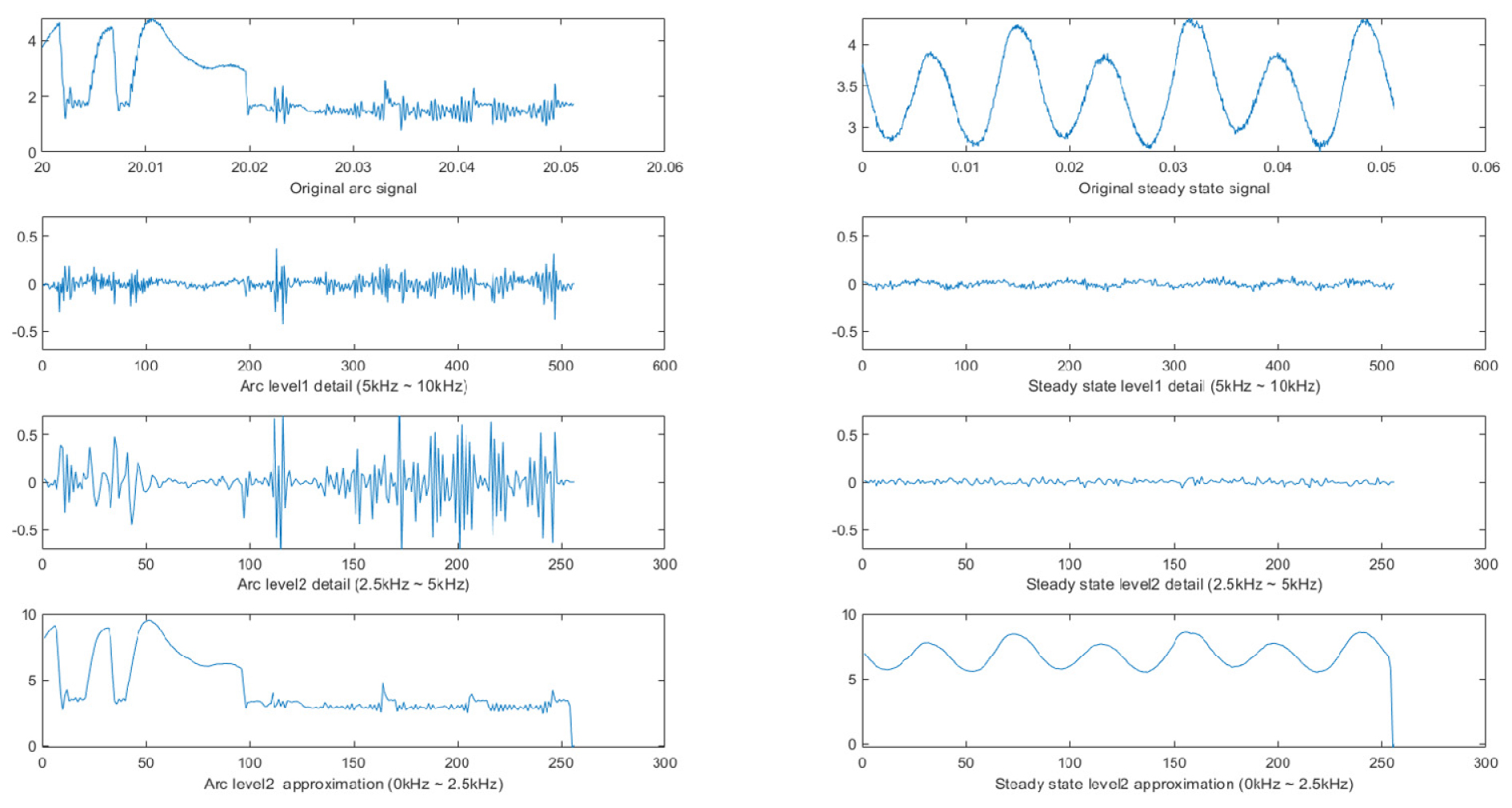
DWT의 경우 Fig. 8의 MRA (Multi-Resolution Analysis) 기법을 사용해서 신호를 특정 주파수 대역으로 분해할 수 있다. Scaling function과의 convolution으로 approximation coefficient를 구하고 wavelet function과의 convolution으로 detail coefficient를 구한다5). 이는 각각 저주파 통과 필터(Low pass filter)와, 고주파 통과 필터(High pass filter)를 통과시키는 과정과 유사하다. 따라서 계수들은 Fig. 9와 같은 filter-bank를 반복적으로 적용해서 얻을 수 있다. 본 연구에서는 Level 1 coefficient (5 ~ 10 kHz)와 Level 2 coefficient (2.5 ~ 5 kHz)를 사용한다.
4.3 에너지 계산(Parseval theorem)
파서벌 정리(Parseval theorem)란 시간 영역의 신호들의 에너지/전력이 주파수 영역의 신호들의 에너지/전력과 같다는 이론이다. 따라서 FFT 또는 DWT를 사용해서 주파수 영역으로 변환된 신호 값들을 토대로 신호의 에너지를 구할 수 있다. 우리는 1,024개의 입력 신호의 에너지가 Threshold를 넘으면 아크라고 판단한다.
5. MATLAB 시뮬레이션
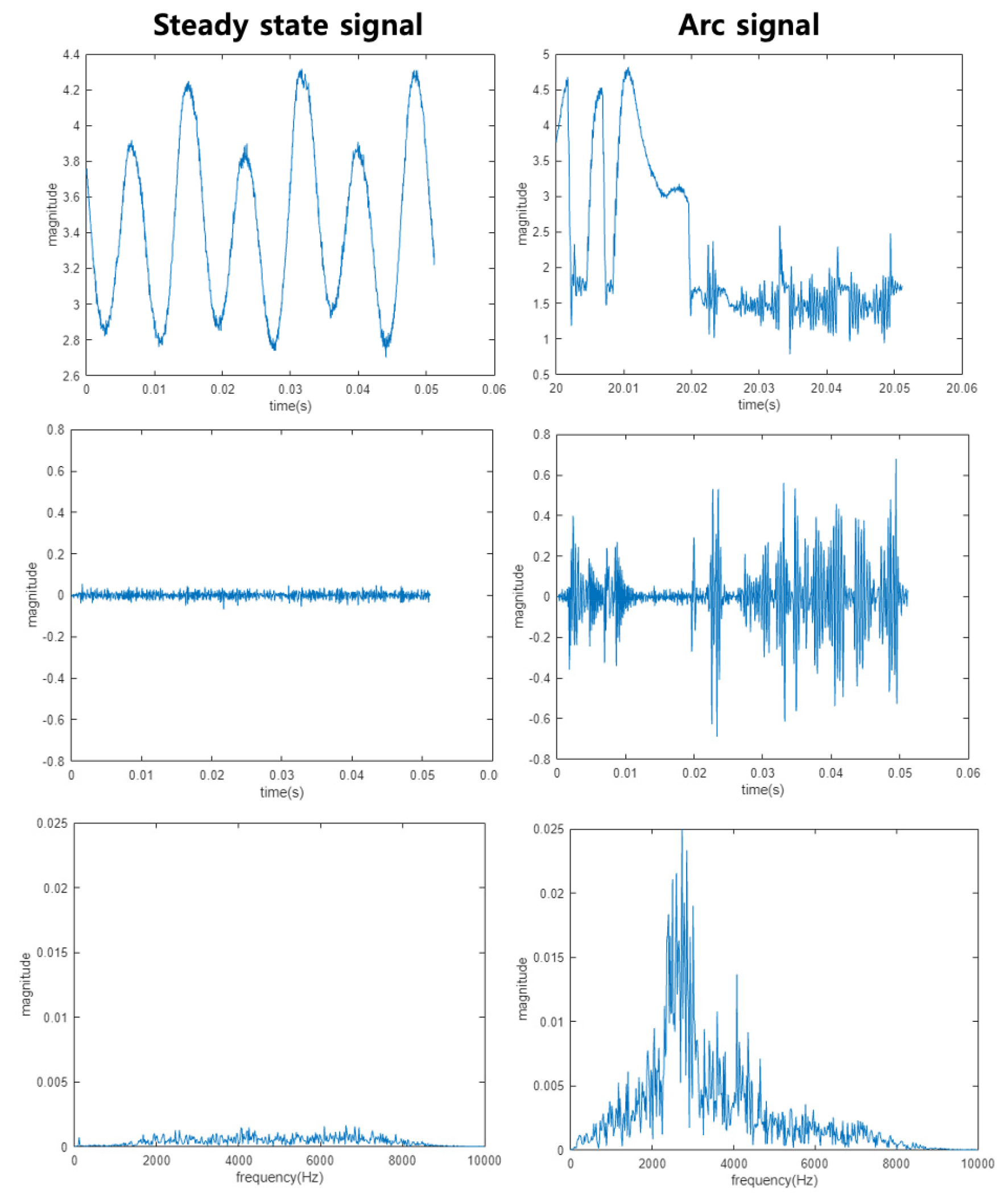
제안된 주파수 분석 방법인 FFT와 DWT에 대한 타당성을 MATLAB 시뮬레이션을 통해 확인하였다. 2016 43번째 IEEE 컨퍼런스(PVSC) 보고서는 태양광 DC 직렬 아크 전류의 고조파 변화는 거의 없으며 저주파(10 kHz 미만)에서도 크기가 작은 아크 전류 신호를 감지 가능하다고 보고했다2). 따라서 Fig. 10의 DC 직렬 아크 전류 파형을 참고하여 Fig. 11과 같이 DC 직렬 아크 전류 신호를 모사했다.
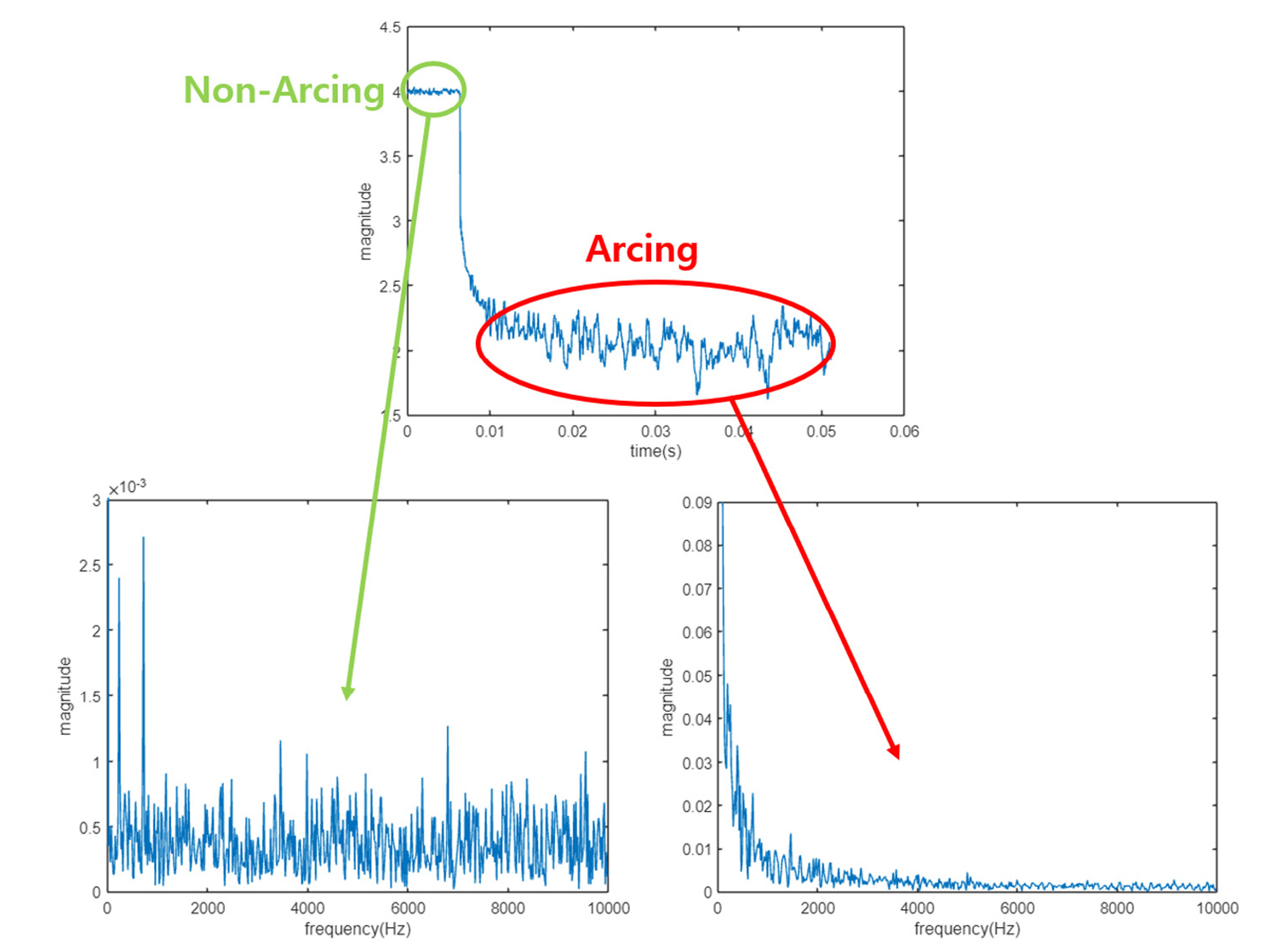
Fig. 11에서 정상상태 전류와 아크 전류의 FFT 기법을 사용해 주파수를 분석한 결과를 보면 아크 전류는 10 kHz 미만의 저주파 대역에 있음을 확인할 수 있다. 또한 정상상태에서의 크기보다 아크 전류의 크기가 더 큰 것을 확인할 수 있다.
5.1 FFT 기법
Fig. 11의 모사한 DC 직렬 아크 전류의 신호를 20 kHz로 샘플링하고 ADC (Analog to Digital Converter)를 통과한 1,024개의 신호라고 가정하였다. IEEE PVSC 레포트는 저주파수 구분을 제안하였으므로 디지털 대역 통과 필터(2.5 kHz ~ 15 kHz)를 적용하였다. 대역 필터를 통과한 신호와 FFT 결과는 Fig. 12와 같다.
Fig. 12의 왼쪽은 필터를 통과한 DC 직렬 아크 전류 신호이고 오른쪽은 FFT 분석 결과이다. FFT 결과를 보면 원하는 대역의 신호만 통과된 것을 확인할 수 있다.
5.2 DWT 기법
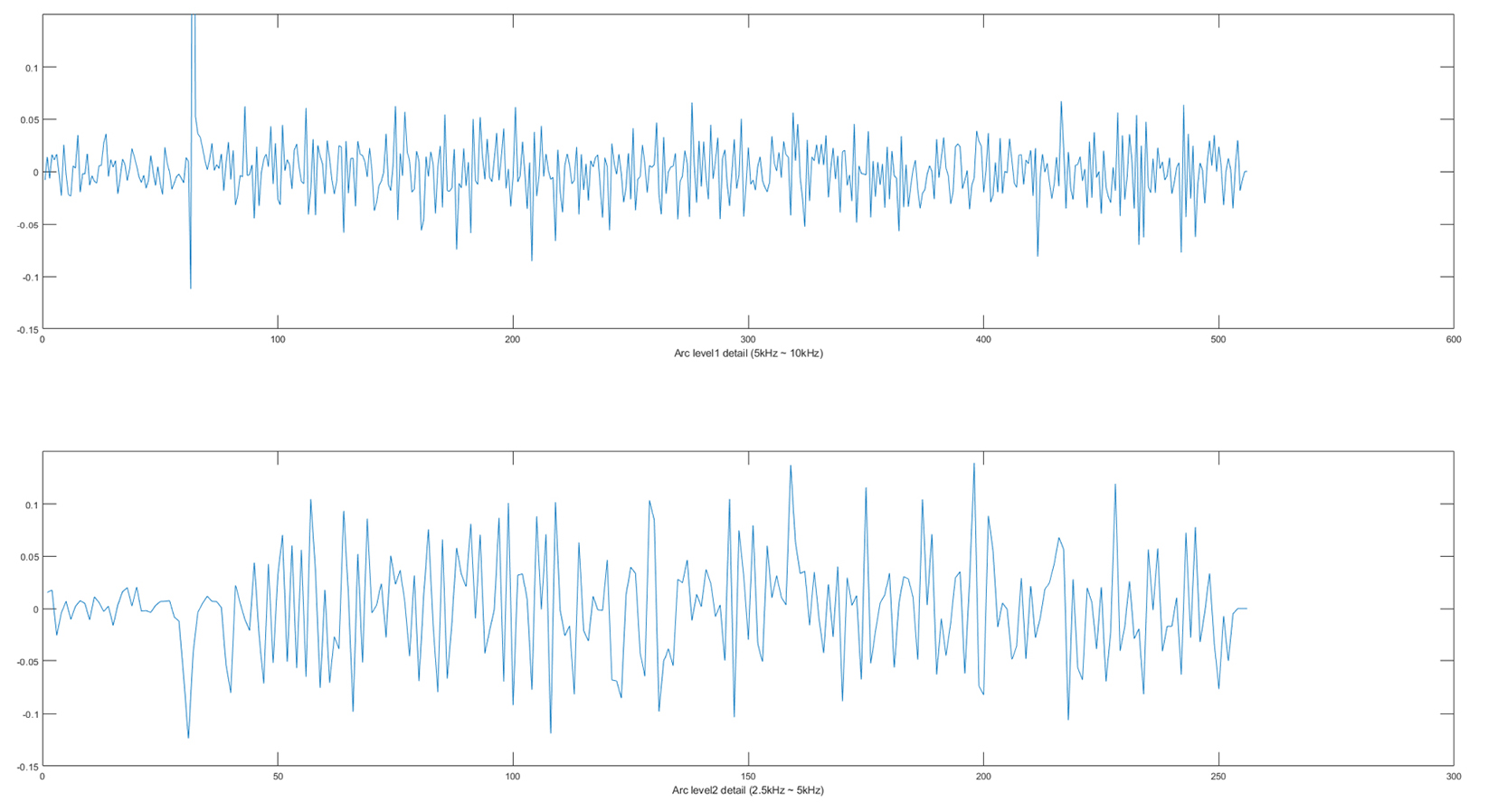
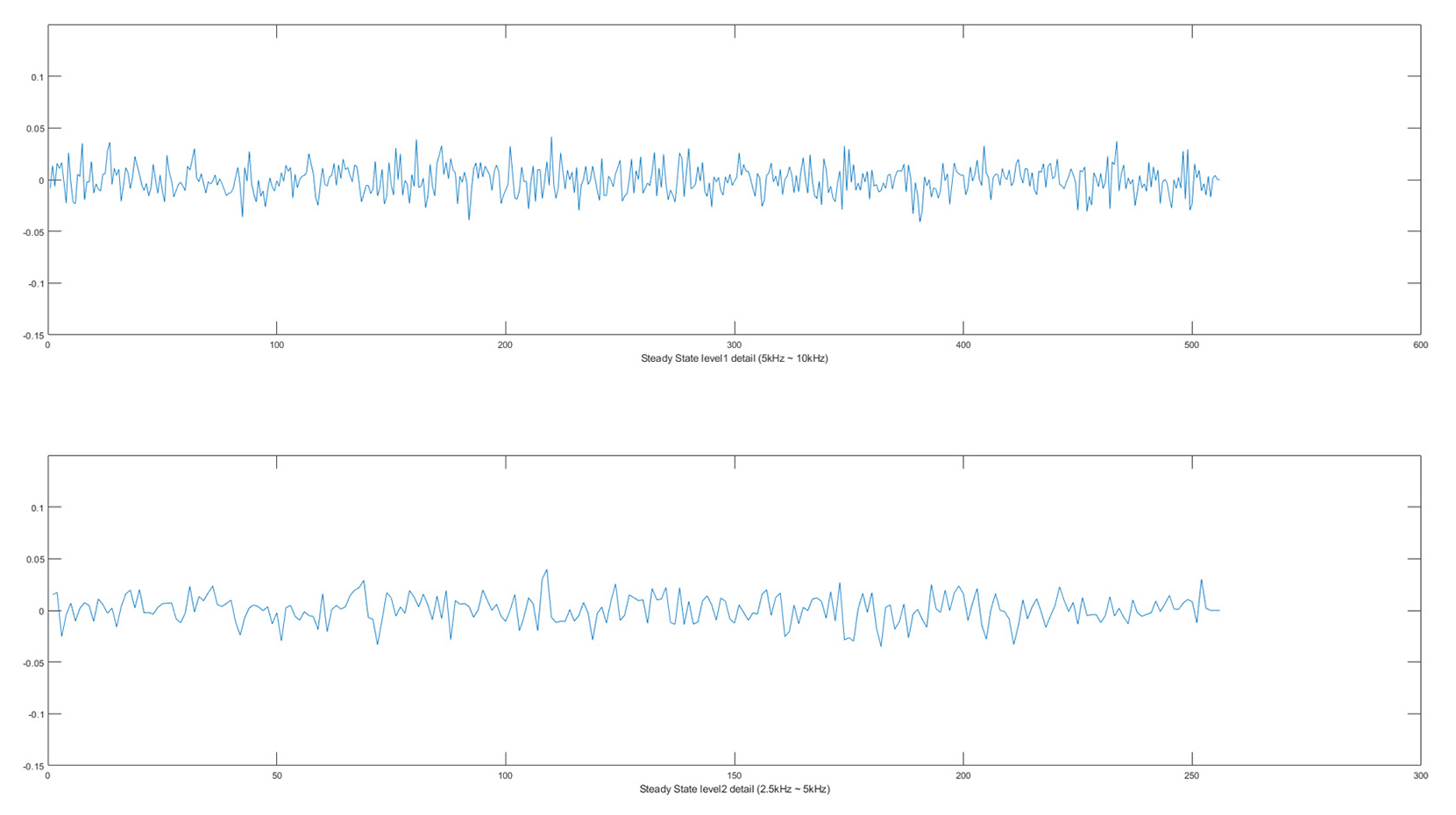
DWT (mother wavelet: Daubechies 4) 기법의 MSD (Multi-level Signal Decomposition) 작업을 통하여 Level 1 (A1, D1)부터 Level 2 (A2, D2)의 값으로 분류한다. 본 연구에서는 디지털 필터를 적용한 FFT와 동일한 조건에서 주파수 분석을 하기 위해 Level 1_D1 (5 ~ 10 kHz)와 Level 2_D2 (2.5 ~ 5 kHz)의 값만 사용한다. Fig. 13과 Fig. 14는 각각 DC 직렬 아크 전류 신호와 정상상태 전류 신호의 DWT 수행 결과이며, 순서대로 Level 1 detail 신호와 Level 2 detail 신호이다.
주파수 분석 결과를 보면 FFT 결과와 마찬가지로 DC 직렬 아크 전류 신호의 크기가 더 큰 것을 확인할 수 있다. 인버터 노이즈는 두드러지게 관찰되지 않는다.
6. 실험 및 검증
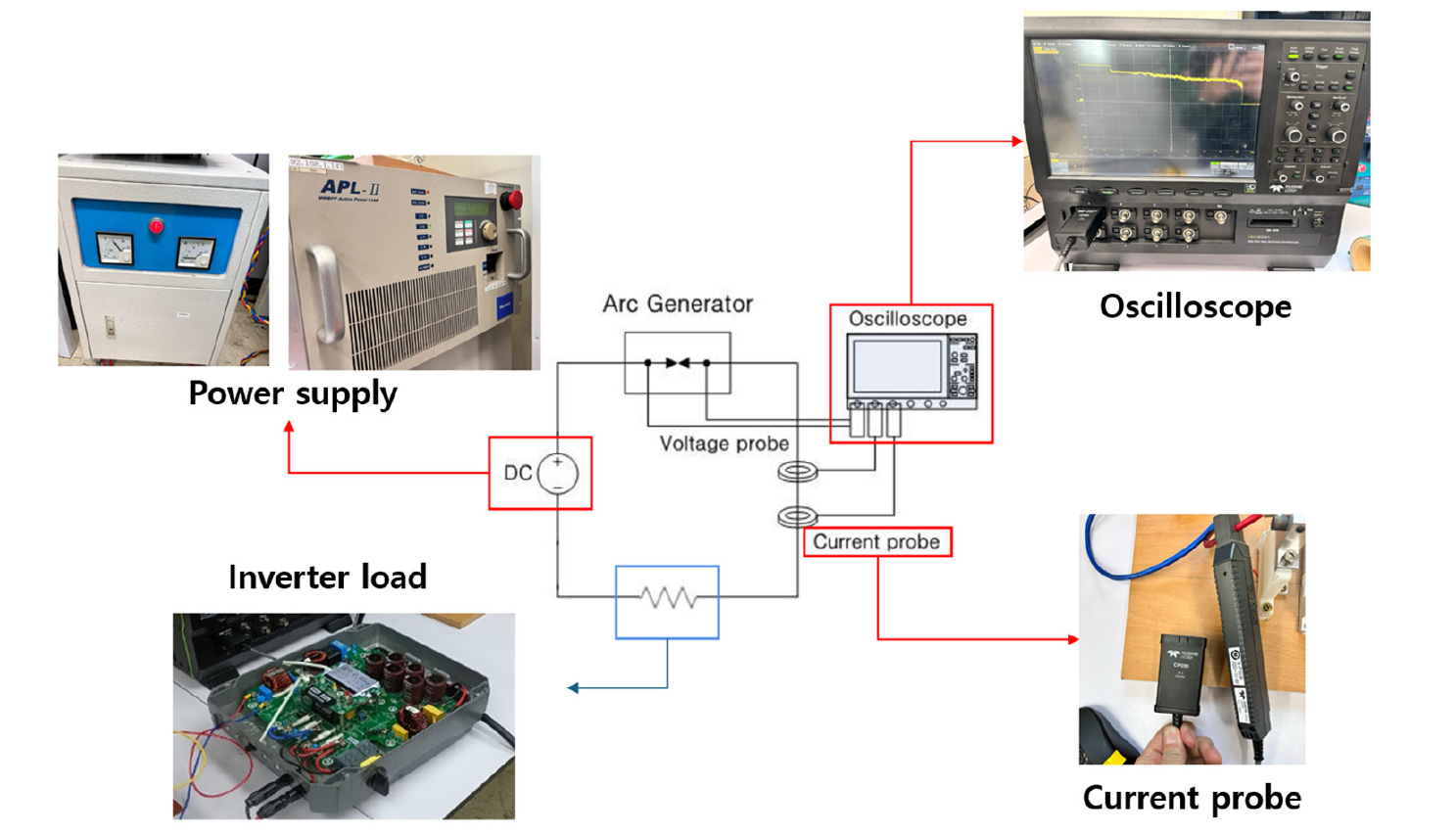
앞서 설계한 아크 검출 알고리즘의 성능을 분석하기 위해 제작한 DC 직렬 아크 발생기를 이용하여 Fig. 15와 같이 아크 발생 실험 세트를 구성하였다. 실험을 통해 아크 발생 시 나타나는 DC 직렬 아크 전류의 특성을 확인한다. 실험 세트는 직류전원(APL), 아크 발생장치, 단상 인버터 부하(S3R7K- 8, 3.7 kW), DC 아크 전류를 측정하기 위한 오실로스코프(TELEDYNE, HDO8058A)와 전류프로브(TELEDYNE, CP030, 30A)로 이루어진다. 실험은 Tables 2, 3과 같이 UL1699B 아크 시험조건을 기반으로 한다. 이때 아크 에너지는 750 J을 넘지 않으며, 2.5초 이내에 아크를 차단해야 한다.
Table 2
UL1699B ED1 (2018), Arcing tests condition
| Minimum Iarc [A] | Current [A] | Voltage [V] | Sep.rate [mm/s] | Gap [mm] |
| 2.5 | 3.0 | 312.0 | 2.5 | 0.8 |
Table 3
UL1699B ED1 (2018), Pass criteria
| Test Standard | Interrupting Time [s] | Arc Energy [J] |
| UL1699B 2018 | 2.5 | 750 |
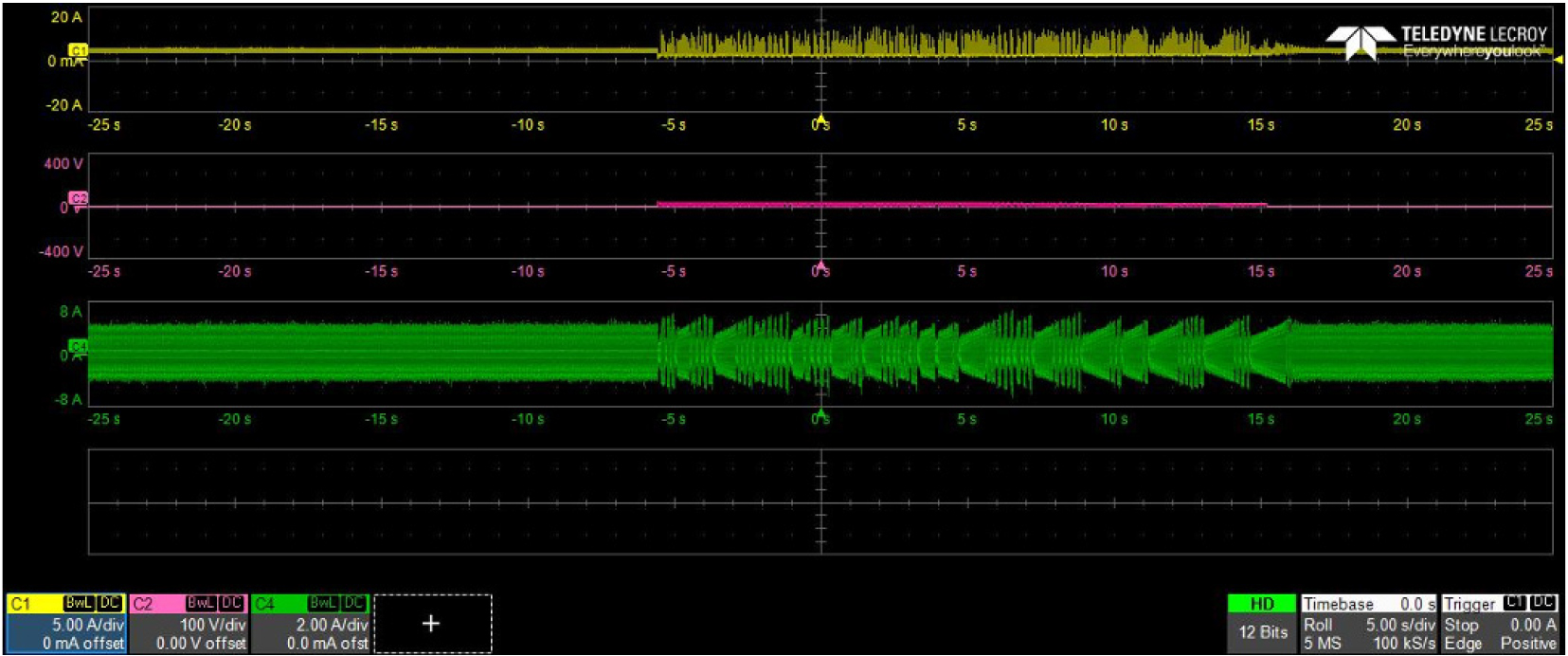
실험순서는 직류전원에서 전극을 공급하고, 아크 발생장치의 이동전극 속도, 전극간격을 시험조건에 맞게 제어하여 이동전극을 이동시켜 아크를 발생시킨다. 이동전극을 2.5 mm/s 속도로 0.8 mm 간격에서 발생한 DC 직렬 아크는 Fig. 16과 같으며, 실험 파형은 Fig. 17과 같다.
Fig. 17의 실험 파형은 Table 2의 UL1699B 조건에서 아크 전류(C1, 노란색), 아크 발생기의 양단 전압(C2, 분홍색), 인버터 출력 전류(C4, 초록색)을 나타낸다. Fig. 17과 같이 아크가 발생하는 순간 전극 양단에서는 아크의 임피던스 발생으로 인한 전압강하가 발생하고, 인버터 전류는 감소한다.
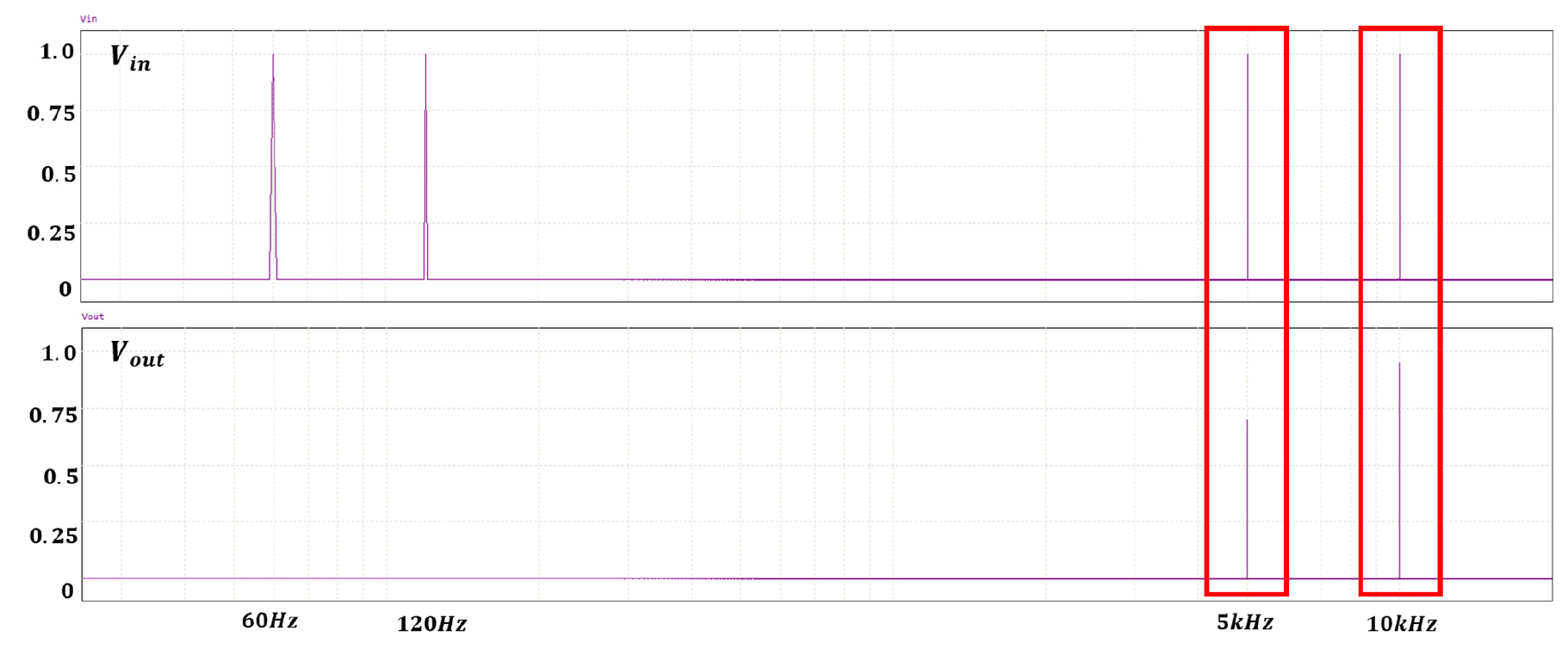
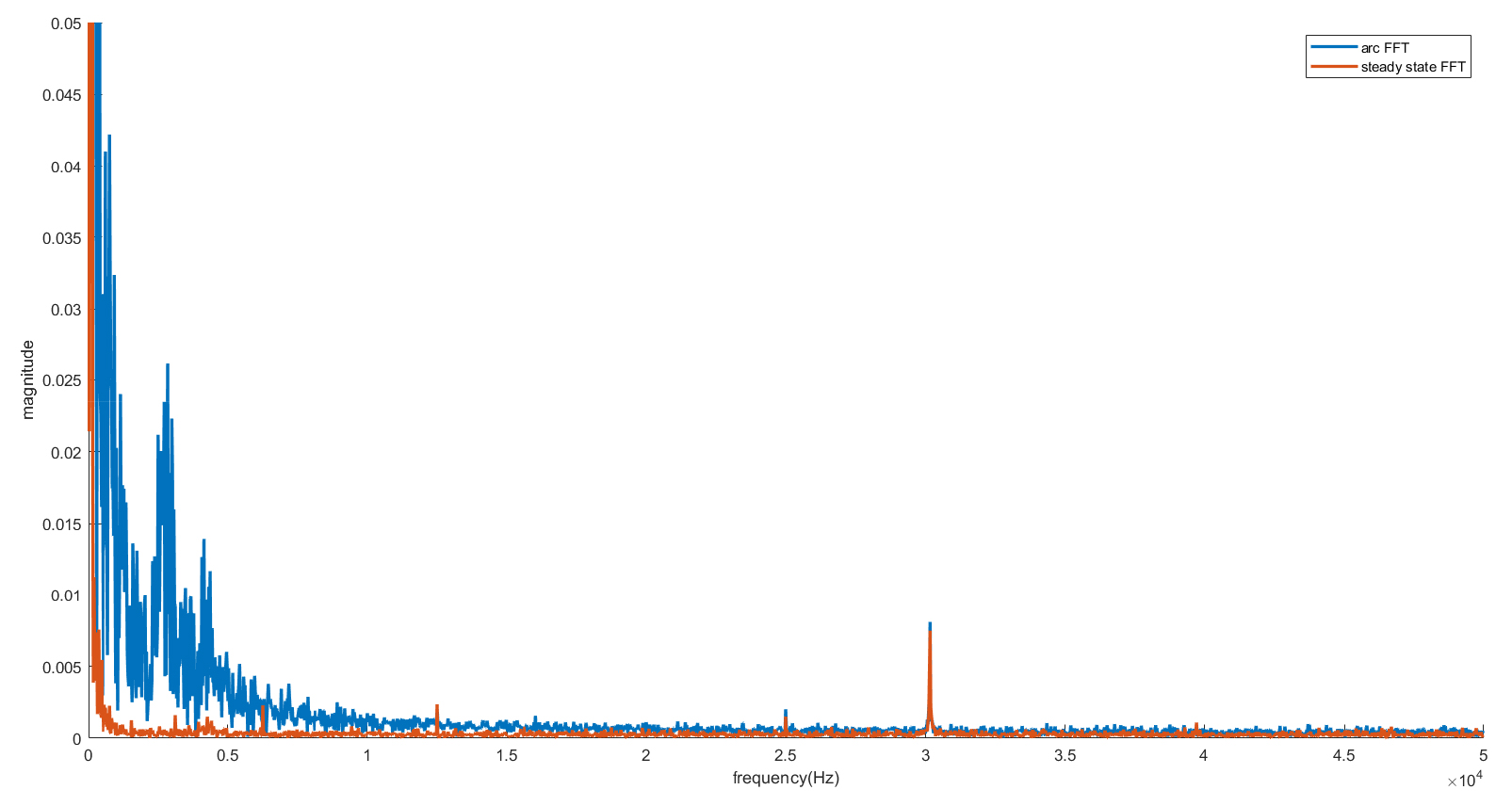
Fig. 18은 정상상태 전류(주황색) 신호와 아크 전류(파란색) 신호의 주파수 분석 결과이다. 정상상태 노이즈가 아크 노이즈에 중첩되는 것을 확인할 수 있고, 약 30 kHz의 인버터 노이즈 성분이 있는 것을 확인할 수 있다. 본 연구에서는 샘플링주파수가 20 kHz이므로 Nyquist 이론에 의해 인버터 노이즈는 두드러지게 나타나지 않는다.
아크 검출 과정은 Fig. 19의 Flowchart와 같다. DC 직렬 아크가 발생하면 ADC를 통해 1,024개 신호의 데이터가 저장된다. 원하는 주파수 대역의 신호를 얻기 위해 대역 통과 필터를 적용하고 FFT 또는 DWT 기법을 사용해서 주파수 분석을 한다. 신호의 에너지가 Threshold를 넘지 못하면 다음 1,024개의 데이터를 받아서 에너지를 계산한다.
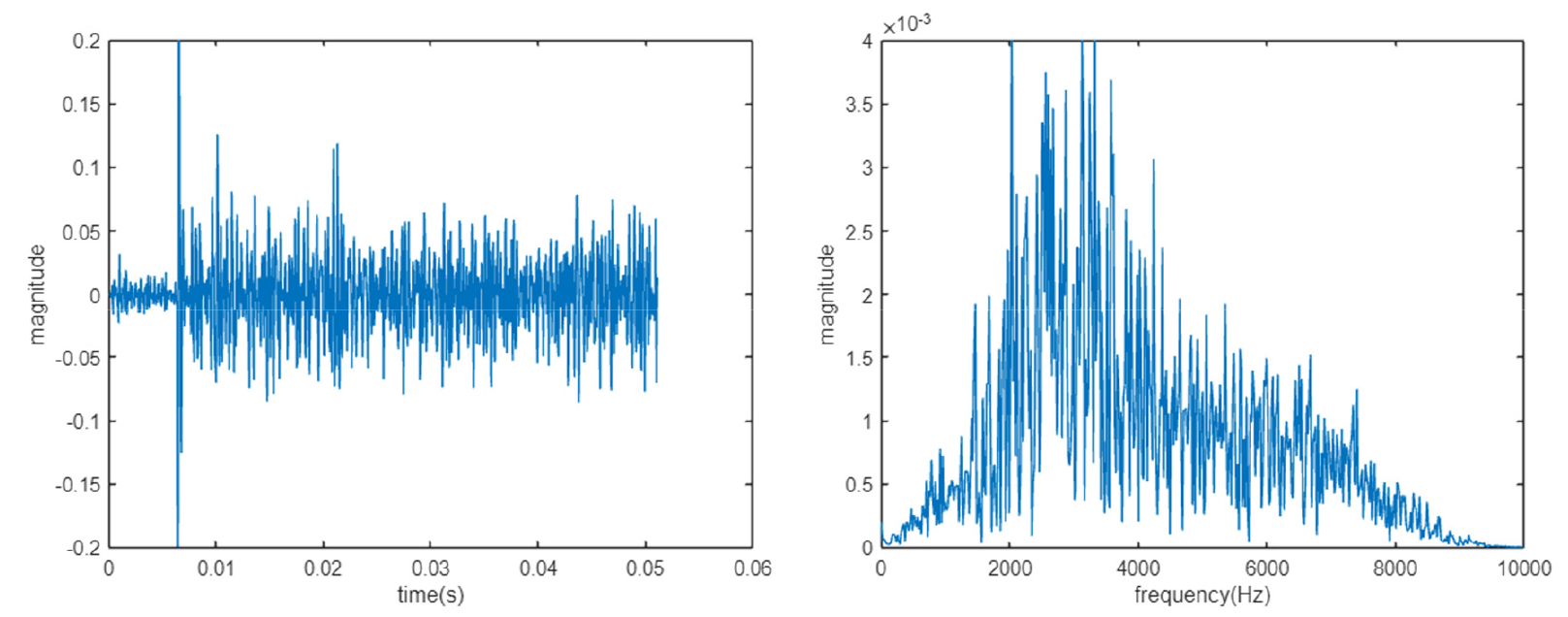
먼저 20 kHz로 샘플링한 처음 1,024개의 데이터를 필터링하고 FFT 기법을 사용하여 주파수 분석을 한다. 분석 결과는 Fig. 20과 같다.
Fig. 20의 왼쪽은 아크가 발생하지 않은 정상상태에서의 선로 전류 신호이고 오른쪽은 아크가 발생한 상태에서 측정된 직렬 아크 전류 신호이다. 위에서부터 순서대로 원본 신호, 대역필터를 거친 신호, FFT 결과이다. FFT 결과를 보면 DC 직렬 아크 전류의 주파수 성분이 저주파수 대역인 약 2 kHz ~ 5 kHz에서 두드러지는 것을 확인할 수 있다.
다음으로 20 kHz로 샘플링한 1,024개의 데이터를 DWT 기법을 사용하여 주파수 분석을 한다. 본 연구에서는 Level 2까지의 DWT를 수행한다. 1회 DWT를 수행하면 Level 1의 고주파 신호(5 ~ 10 kHz)와 저주파 신호(0 ~ 5 kHz)를 얻을 수 있으며, 저주파 신호를 다시 1회 DWT를 수행하면 Level 2의 고주파 신호(2.5 ~ 5 kHz)와 저주파 신호(0 ~ 2.5 kHz)를 얻을 수 있다. 이처럼 DWT를 통해 추출된 신호는 대역필터와 같은 기능을 하기 때문에 특정 주파수 대역만을 선택적으로 분석할 수 있어 아크 검출에 용이하다.
위 과정을 주파수 대역에서 보면 Fig. 21과 같으며, DWT 분석 결과는 Fig. 22와 같다. 왼쪽은 아크가 발생한 상태에서 측정된 직렬 아크 전류 신호이고, 오른쪽은 아크가 발생하지 않은 정상상태 직렬 아크 전류 신호이다. ADC된 신호, Level 1detail (5 kHz ~ 10 kHz), Level 2 detail (2.5 kHz ~ 5 kHz) 신호, Level 2 approximation (0 ~ 2.5 kHz)를 순서대로 나타내었다. 약 30 kHz의 인버터 노이즈는 분해한 주파수대역에 속하지 않기 때문에 두드러지게 나타나지 않는다. 본 연구에서는 Level 1과 Level 2의 detail 신호만을 아크 검출에 활용한다.
마지막으로 신호의 에너지를 계산하여 아크를 검출한 결과는 Fig. 23과 같다.
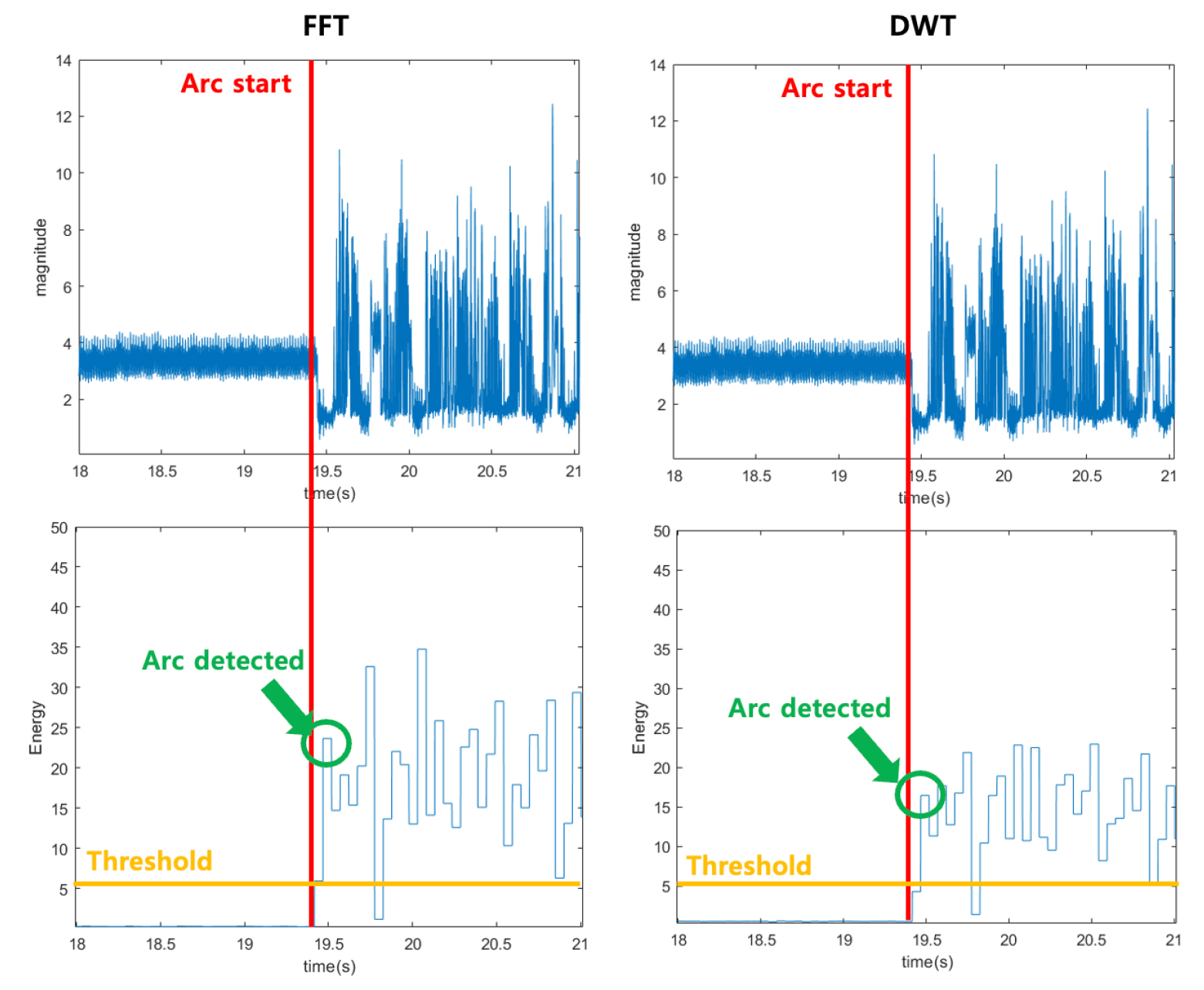
Fig. 23의 왼쪽은 FFT, 오른쪽은 DWT를 사용해서 신호의 에너지를 계산하고 아크를 검출한 결과이다. 아크가 발생하기 전에는 에너지가 0에 가깝다가 아크가 발생하면 에너지가 급격하게 증가하는 것을 확인할 수 있다. Threshold를 약 5 J로 설정하면 FFT와 DWT 모두 두 번째 1,024개의 데이터에서 아크 검출이 가능하다. FFT의 에너지가 정상과 아크 간에 약 250배의 에너지 차이를 보이며 DWT의 경우 Level 1, Level 2 detail coefficient로부터 계산한 에너지가 정상과 아크 간에 약 170배의 차이를 보인다. 이는 설계한 알고리즘이 아크를 정확히 검출할 수 있음을 의미한다.
Table 4를 보면 FFT의 곱셈 연산량이 DWT에 비해 약 36% 더 많으며 대입 연산량은 약 13배 정도 더 큰 것을 알 수 있다. 곱셈의 크기, 데이터 형태, MCU의 구조, RAM과 캐시 메모리의 사용 여부에 따라 다르겠지만 통상적으로 메모리에 접근하는 대입 연산이 곱셈 연산에 비해 연산 시간이 더 걸린다고 알려져 있다. 두 알고리즘으로부터 곱셈 횟수와 대입 횟수를 비교해 보았을 때 곱셈 횟수와 대입 횟수가 더 많은 FFT 가 DWT에 비해 연산 시간이 더 길다.
7. 결 론
본 연구에서는 UL1699B 아크 시험조건을 기반으로 실험을 진행하였고, 낮은 샘플링 주파수 20 kHz에서 DC 직렬 아크 전류의 주파수 특성을 빠르게 분석하고 식별하기 위해 최근 주파수 분석 방법 중 가장 널리 쓰이는 Fast Fourier Transform (FFT)과 Discrete Wavelet Transform (DWT), 두 주파수 분석 방법을 비교 분석하였다. 또한 DC 직렬 아크 검출에 저주파(10 kHz 이하) 신호를 사용하는 경우에도 정상상태 신호의 에너지보다 약 100배 이상 크기 때문에 아크 검출이 가능함을 확인하였다.
FFT와 DWT 두 방법 모두 샘플링 주파수가 20 kHz일 때 1,024개의 데이터를 샘플링하는 시간은 51.2 ms이다. FFT와 DWT 기법을 사용할 경우, 아크 검출시간은 각각 80 ms, 71 ms로 연산량이 더 적은 DWT 기법이 조금 더 빠른 것을 확인할 수 있다. 두 방법 모두 UL1699B 아크 검출기의 아크 검출 및 소호 시간 기준 2.5초 이내를 충분히 만족하는 성능을 검증하였다.
FFT 알고리즘의 경우 라이브러리가 보편화되어 있어 알고리즘 설계가 용이하며 병렬 연산이 유리하기에 FPGA 상에서 구현할 시 더 빠른 연산속도를 기대할 수 있다. DWT 알고리즘의 경우 계산량이 적어 MCU 상에서 FFT에 비해 빠른 계산 속도를 기대할 수 있다. 하지만 웨이블릿 함수를 메모리에 상시 저장하고 있어야 한다는 단점이 있다.
낮은 주파수 대역에서도 크기가 작은 아크 전류를 감지할 수 있음으로 기존 차단기에 비해 약 10 ~ 20배 비싼 AFCI (Arc Fault Circuit Interrupter)의 가격을 낮출 수 있다. 실제 아크 차단기에 쓰이는 연산 장치마다 연산속도에 차이가 있을 수 있으며 아크 검출 후 기계적 차단까지 걸리는 시간 등을 고려해야 한다는 점에서 실험 및 추가적인 연구가 필요하다.