1. 서 론
2. 방법론
2.1 State-space formulation
2.2 LTI (Linear time invariant) / LTV (Linear time variant)
3. 건물 모델링
3.1 대상건물 / 실내, 실외 데이터
3.2 Grey-box 모델링
4. MPC 시뮬레이션
5. 결 론
6. 향후 연구 과제
기호 및 약어 설명
T : Temperature (℃)
R : Resistance (m2‧K/W)
Cp : Specific heat capacity (kcal/kg‧℃)
Q : Heating and Cooling energy (W)
α : Absorption coefficient
Cn : Regression coefficient (n = 1,2,3,4)
Idesign : Design infiltration rate (m3/s)
Fschedule : User defined schedule
Wf : Wind direction modifier
Rf : Surface roughness multiplier
P : Perimeter of the surface (m)
V : Wind speed (m/s)
A : Area of the surface (m2)
hf : Forced convective heat transfer coefficient (W/m2‧K)
hn : Natural convective heat transfer coefficient (W/m2‧K)
hc : Surface exterior convective heat transfer coefficient (W/m2‧K)
MPC : Model-based prediction control
LTI : Linear time invariant
LTV : Linear time variant
하첨자 설명
room : Indoor room air
out : Outdoor
env : Envelop
oe : Between outdoor and envelop
er : Between envelop and room
rc : Between room and corridor
inf : infiltration
cor : Corridor
sol : Solar radiation
LGT : Light
refri : Refrigerator
comp : Computer
ahu : Air handling unit
meas : Actual measurement
exp : Experiment
k : Timestep
Opt : Optimal feedback control
Feed : Conventional feedback control
1. 서 론
국토교통부의 ‘건축물에너지사용량 통계’에 따르면 건물에너지 사용량은 18년(34,442 천TOE), 19년(33,572 천TOE), 20년(33,187 천TOE)으로 갈수록 점차 감소하는 추세이며1), 한국전력공사에 따르면 물가 상승으로 전기요금 인상률은 1982년도부터 2020년도까지 47.1%로 점차 증가하는 추세이다2). 2050년까지 탄소중립을 실현하기 위해서는 건물에너지 사용량 및 전기비용의 절감이 필요하다. 이를 위한 부하예측 및 진단/평가와 관련된 다양한 연구3,4)가 수행되어 왔다. 본 연구는 건물 냉난방 시스템의 효율적인 관리 및 제어를 위한 방법으로써 모델기반 예측제어(Model-based Predictive Control, 이하 MPC)를 제안하며 이를 위한 모델링 및 시뮬레이션 결과를 분석한다.
MPC를 위한 건물에너지 시뮬레이션 기법은 white-box, grey-box, black-box 세 방법으로 나뉠 수 있다. White-box는 EnergyPlus, TRNSYS 등 building energy simulation tool을 의미한다. black-box는 machine learning 등 시스템의 모델링을 위한 system identification 기반이며 grey-box는 두 모델의 중간 형태이다5). 그 중 white-box 모델 기법은 다른 모델보다 정확한 결과를 가져오지만, 시뮬레이션을 하기에 필요한 parameter가 많아 MPC를 구현하는데 계산 시간이 오래 걸리고, 최적해를 도출하는 것에 어려움이 있다. 또한 black-box는 새로운 데이터에 따라 적응성이 향상된다는 장점이 있지만 누락, 편향된 데이터에 따라서 품질이 낮은 모델로 이어질 수 있다6). 따라서 white-box와 black-box의 성능을 모두 갖춘 모델이면서 white-box 모델 기법보다 더욱 간단한 모델이 필요하며 black-box 모델 기법보다 더욱 해석이 용이한 모델이 필요하다. 이를 위해 본 연구에서 grey-box 모델을 사용하였다. 현재 grey-box 모델 기법은 다수의 연구에서 모델의 정확성 및 적용성이 검증되었으며7,8) 특정 연구에서는 실제 교육용 건물에서의 실제 적용을 통한 우수한 에너지 절감량을 제시하였다9).
본 연구에서는 MPC에서 grey-box 모델의 적용성을 검증하기 위하여 실측 데이터를 이용한 다양한 모델링 방법을 비교/분석 하였다. 구체적으로, 침기 및 대류 열전달과 관련된 현상이 실시간 변하는 모델과 변하지 않는 모델로 각기 다른 모델을 구성하였다. 즉, 파라미터가 주변 환경에 따라 변하지 않는 LTI (Linear time invariant) 모델과 변하는 LTV (Linear time variant) 모델로 나누어 개발하였다. 그 중 MPC에 적용하기 용이하며 동시에 정확성 또한 떨어지지 않는 모델을 선택하여 이를 바탕으로 MPC 시뮬레이션을 수행하였다. 또한 MPC와 최소한의 냉방에너지 사용량을 갖는 가장 이상적인 되먹임 제어(Optimal feedback control), P제어를 통한 일반적인 되먹임 제어(Conventional feedback control)간의 실내온도 및 냉방사용량을 비교하였다. 이를 통해 MPC의 전기비용 절감을 확인하였으며, 국내 다양한 전기비용 구조를 적용하여 다양한 시나리오에서의 정량적인 전기비용 절감량을 도출하였다.
2. 방법론
2.1 State-space formulation
State-space formulation은 물리적 계를 입력, 출력, 상태 변수의 1차 미분 방정식으로 표현하는 수학적 모델이다. 벡터, 행렬 등 수학적 표현이 간결하다는 장점이 있어 본 연구에서는 grey-box 모델에 state-space formulation을 적용하여 사용하였다. 이는 아래와 같이 표현된다. x는 state이고 본 연구에서는 건물의 온도(실내 공기, 외피)이다. 또한 u는 input data(외기온도, 실내기기 소비전력, 에어컨 cooling rate 등)를 의미한다. A와 B matrix는 각각 state, input matrix이다. 각 matrix를 구성하는 값은 건물 모델의 변수로써 건물의 열 저항(Resistance), 열용량(Capacitance) 및 계수이며 이 값들은 최적화를 이용하여 도출된다.
2.2 LTI (Linear time invariant) / LTV (Linear time variant)
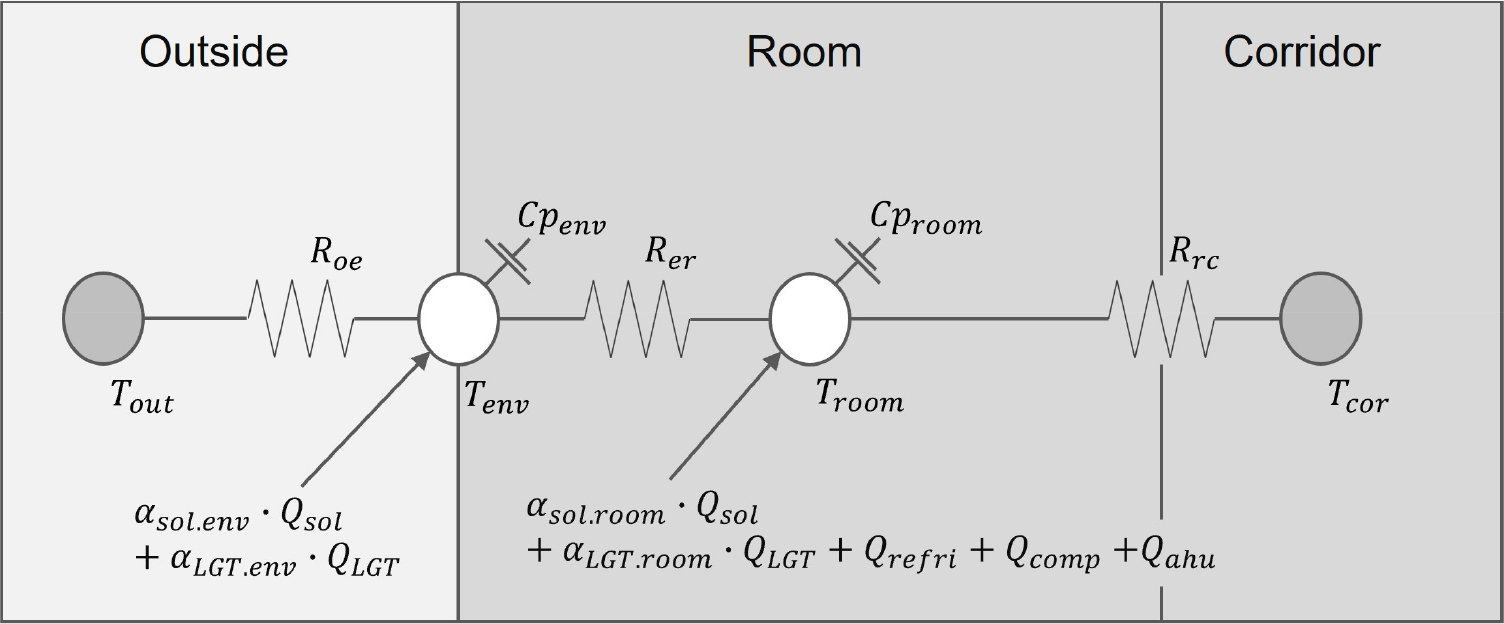
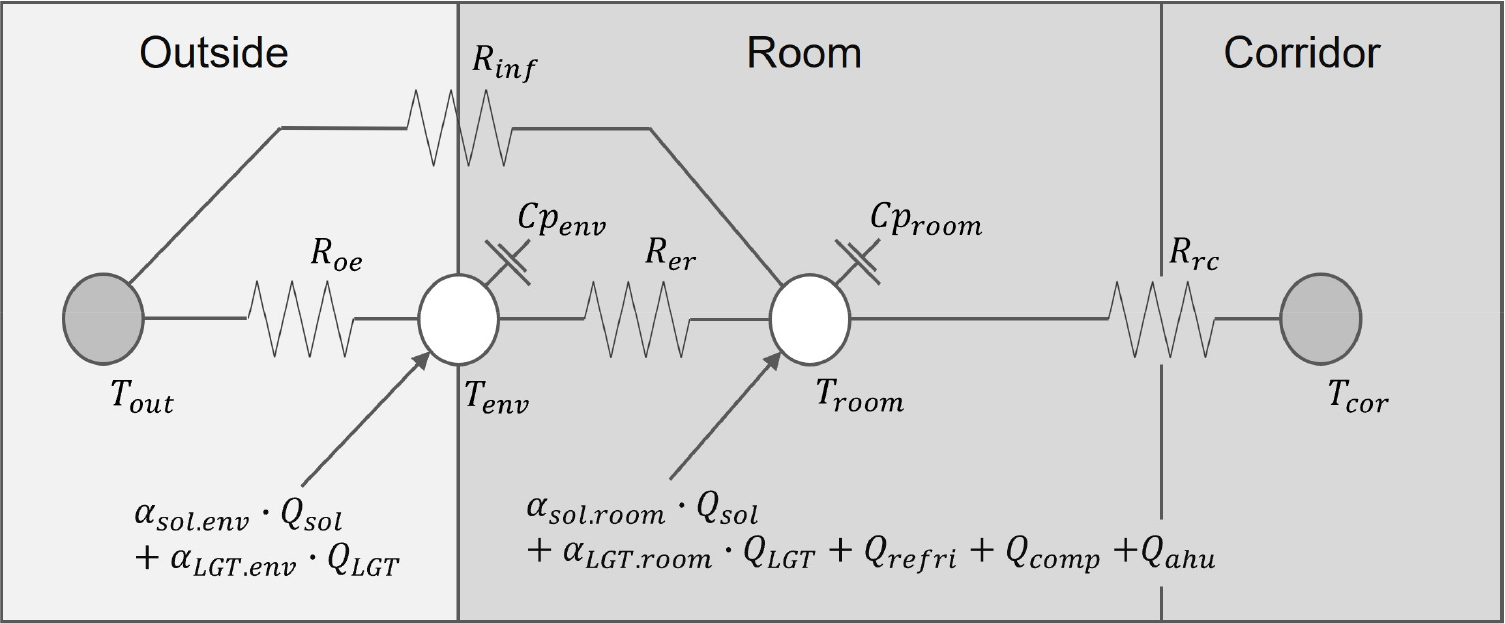
본 모델에서는 grey-box 모델을 MPC 시뮬레이션에 적용하기 위해서 LTI 모델과 LTV 모델의 비교를 실시하였다. LTI는 선형이면서 시불변인 시스템을 의미하며 grey-box 모델로는 기본 모델(case 1)으로 설정하였다. LTV는 선형이면서 시변인 시스템을 의미한다. LTV모델은 침기량을 추가한 모델(case 2)과 가변열저항을 추가한 모델(case 3)로 설정하였다. Figs. 1과 2는 각각 이들의 열 네트워크(R,C circuit)을 나타낸다.
Case2와 3의 LTV 모델에서 사용된 침기 및 대류 열저항 관련 식들은 EnergyPlus에 내장된 식을 사용하였으며 아래와 같다. 침기 모델은 regression 식(2)을 이용하였고10), 대류열전달 식은 BLAST detailed 모델 식(3), (4), (5)을 이용하였다10,11).
3. 건물 모델링
3.1 대상건물 / 실내, 실외 데이터
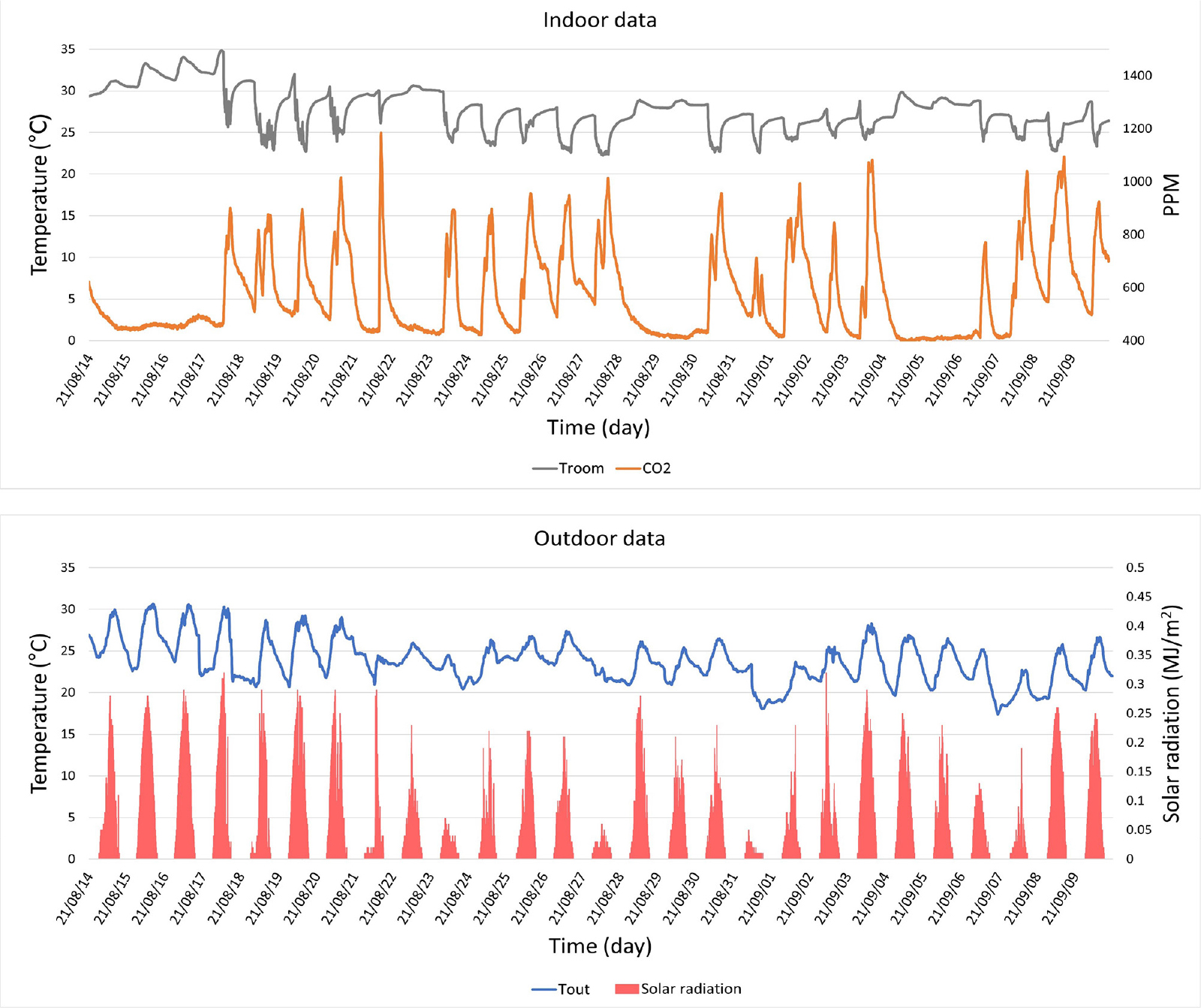
대상 건물은 인천에 위치한 15층 규모의 교육시설 건물이다. 11층(24개의 zone)에서 한 개의 zone을 모델링 하였으며 대상건물과 대상 zone은 Fig. 312)에 나타내었다. Fig. 4은 약 4주간의 실측 자료인 실내 환경 데이터(실내온도, CO2농도)와 기상청 기상자료개방포털13) 자료에서 첨부한 인천광역시의 실외 환경 데이터(외기온도, 일사량)를 나타낸다. 추가로 대상 존의 에어컨을 통한 실시간 냉방 에너지 양은 측정이 불가하여 시스템의 정격용량을 사용하였다. 재실자의 스케쥴은 CO2 농도를 활용하여 간접적으로 계산하였다. 재실 스케쥴에 따른 실내기기 사용량은 플러그에 꽂아서 측정이 가능한 wifi 기반의 전력측정기를 이용하였다. Table 1은 모델링에 사용된 실내기기의 플러그 파워와 에어컨의 정격용량을 보여준다.
Table 1.
Rated capacity of air conditioner and power consumption of indoor equipment (W)
| Category | ON | OFF |
| 4ways Heat Pump | 7096.53 | 0 |
| Computer | 120 | 96 |
| Lighting | 228 | 0 |
| Refrigerator | 76 | 0 |
3.2 Grey-box 모델링
Grey-box 모델은 대상 건물에서 한 개의 zone을 두 개의 상태(state)로 단순화하여 상태공간방정식인 식(1)을 적용하였다. 이는 세 개의 열저항과 두 개의 열용량으로 구성된 3R2C의 형태를 가진 모델이다. LTI (Linear time invariant) 모델과 LTV (Linear time variant) 모델로 모델링 하였으며 LTV 모델은 LTI 모델에 추가적으로 침기량과 가변열저항을 적용하였다.
LTI 모델(case 1)은 Fig. 1로 총 9개의 파라미터(Roe, Rer, Rrc, Cpenv, Cproom, αsol.env, αsol.room, αLGT.env, αLGT.room)를 가지며 시간이 지남에 따라 저항 값이 변하지 않는 모델이다. LTV 모델은 Fig. 2로 침기량을 추가한 모델(case 2)과 가변열저항을 추가한 모델(case 3)로 두 개의 case로 나누어서 나타내었다. 총 13개의 파라미터(Roe, Rer, Rrc, Cpenv, Cproom, αsol.env, αsol.room, αLGT.env, αLGT.room, C1, C2, C3, C4)를 가지며 시간이 지남에 따라 침기량과 저항 값이 변하는 모델이다. 파라미터의 최적화를 위해 matlab의 비선형 최적화 알고리즘인 fmincon 함수를 이용하였다.
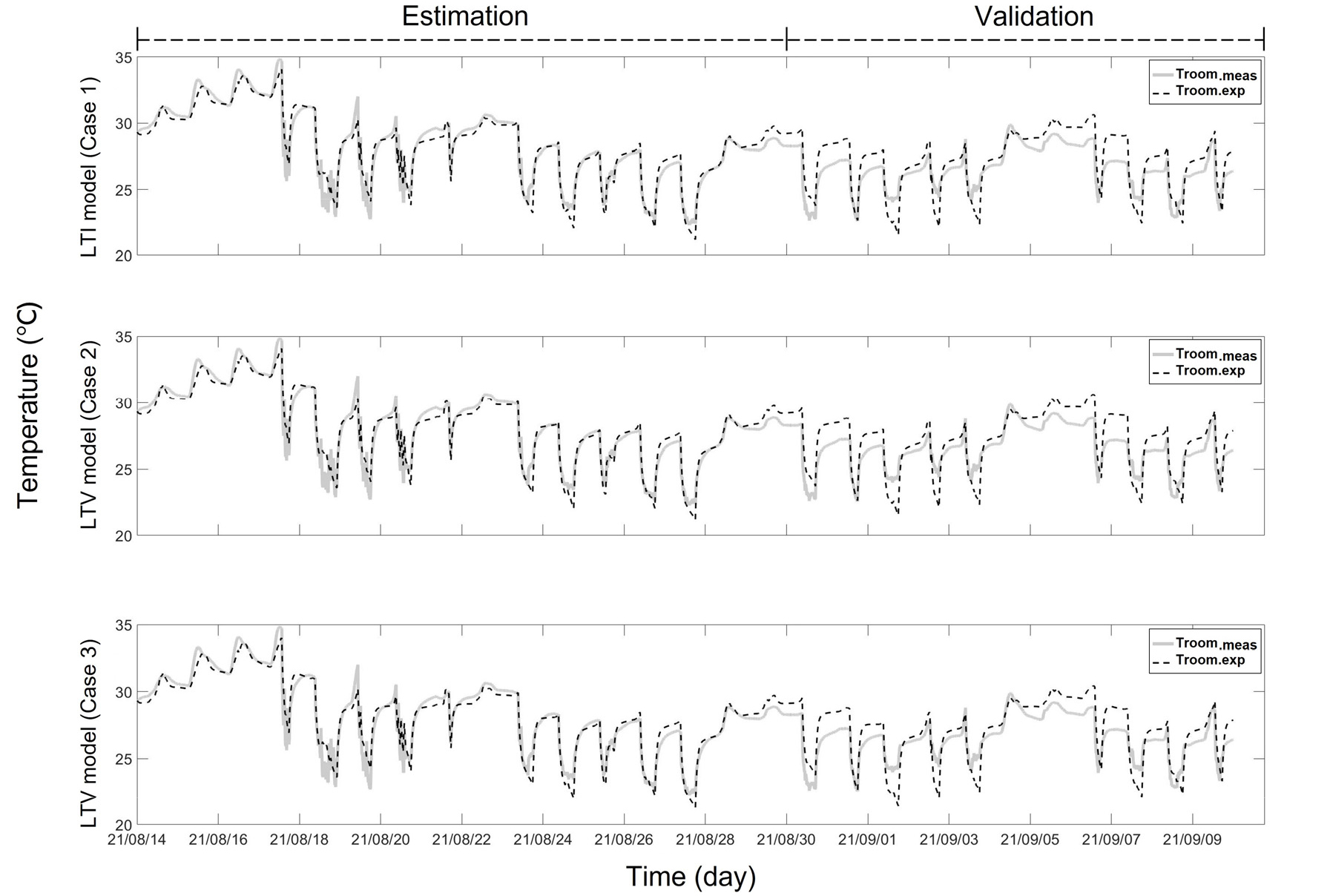
4주간(21.08.14 ~ 21.09.09)의 실측 데이터로 약 2주(21.08.14 ~ 21.08.30)는 Estimation을 하였고 남은 기간(21.08.31 ~ 21.09.09)으로 validation을 하였다. 모델링 결과는 식(6)과 같이 Root Mean Square Error (RMSE)으로 정량화 하였다. Fig. 5는 두 모델의 estimation, validation 결과를 보여주며 RMSE의 값은 Table 2와 같다. LTI와 LTV 모델 모두 RMSE 1℃ 미만의 결과를 보여준다. 현재 온도에 대한 예측성능의 기준은 명확하게 명시되어 있지는 않지만, 본 연구에서의 예측결과는 실측 실내온도의 양상을 1℃ 미만의 차이로 무리 없이 따라가는 것을 보여주며 이는 준수한 예측결과라고 말할 수 있다. Validation 평가에서 LTV 모델이 LTI 모델보다 향상된 결과를 보이지만 상호간의 RMSE 차이가 작은 것을 볼 수 있다. 또한 grey-box 모델을 MPC 시뮬레이션에 적용할 때 LTI 모델은 수학적 해를 도출할 수 있는 선형계획법을 사용할 수 있지만, LTV 모델은 비선형 최적화를 사용해야하는 어려움이 있다. 따라서 MPC 시뮬레이션에는 예측성능이 준수하면서 MPC에 적용하기 용이하며 수학적으로 해를 도출할 수 있는 LTI 모델을 선택하여 적용하였다.
4. MPC 시뮬레이션
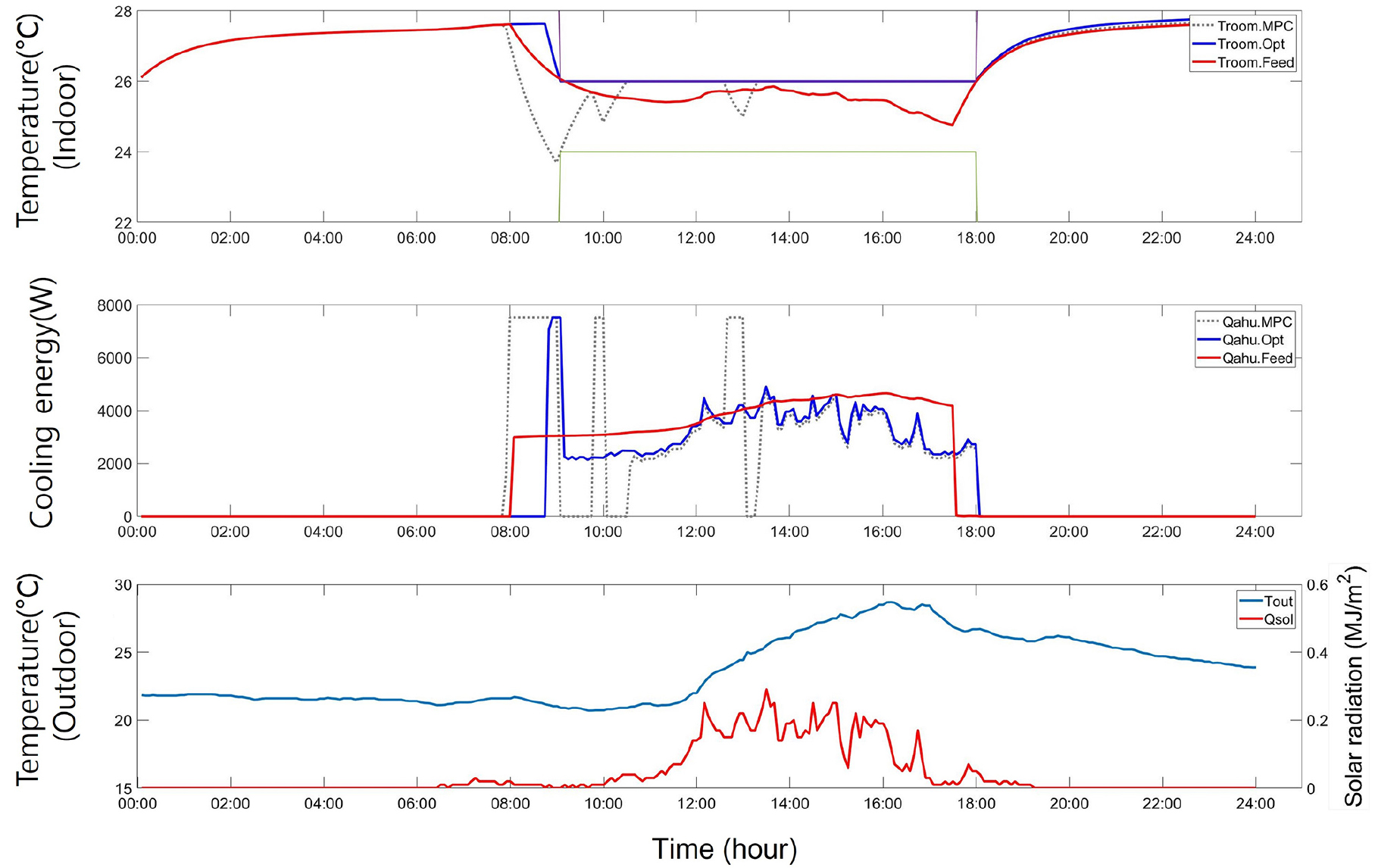
MPC 시뮬레이션은 pre-cooling을 하여 전기비용을 낮추기 위한 목적으로 진행되었다. 시뮬레이션 기간은 하루동안 진행되었으며 초기온도, comfort bound가 포함된 MPC 시뮬레이션 결과(실내온도, cooling energy)는 Fig. 6와 같이 나타내었다. 목적함수는 하루 중 사용된 전기비용의 합으로 설정하였으며 LTI 모델을 적용하였다. 또한 다양한 전기비용 구조(Table 3, Table 4)를 적용하여 이에 따른 정량적인 전기비용 절감량을 비교/분석하였다.
Table 3은 일반용 건물, 교육용 건물에서의 전기비용 구조를 보여준다. High voltage의 구분은 high voltage A (표준전압 3,300 V 이상, 66,000 V 이하), high voltage B (표준전압 154,000 V), high voltage C (표준전압 345,000 V 이상)와 같이 표준전압의 차이로 나타내어진다. 추가로 selection은 selection I (전기사용시간이 월 200시간 이하), selection II (전기사용시간이 월 200시간 초과, 500시간 이하), selection III (전기사용시간이 월 500시간 초과)으로 구분된다. Light load, intermediate load, maximum load인 계절별 시간대의 구분은 Table 4와 같이 나타난다. 시뮬레이션은 동일한 건물 모델을 이용하여 다음과 같은 세 가지 제어 방식을 적용하여 수행하였다.
∙Conventional feedback : 되먹임 제어에서 P제어를 이용한 간단한 제어 규칙을 적용하였다. 일반적인 되먹임 제어이며, cooling energy 사용량에 일정 계수를 곱하여 나타내었다. 또한 실내 온도가 comfort bound 내에 위치하도록 스케쥴 조정을 하였다.
∙Optimal feedback : MPC와 같은 최적화 식을 적용하였으나 목적함수의 값이 전기사용량이 아닌 cooling energy 사용량이다. 따라서 시뮬레이션 결과에서 실내 온도는 upper comfort bound와 정확히 일치한다. 냉방기의 운영에 있어서 미리 가동 및 종료 하는 것 까지 모사된 최적의 되먹임 제어를 가정한다.
∙MPC : 본 연구의 최적화 기법을 적용한 MPC 케이스이다.
Table 3.
Electricity cost for general and educational buildings, Applicable from April 1, 2022 (June to August)
Table 4.
Load time zone by season
Fig. 6의 indoor temperature 그래프에서 MPC의 결과는 conventional feedback control, optimal feedback control의 결과와는 달리 pre-cooling을 하는 것을 볼 수 있다. Table 3, Table 4에서 볼 수 있듯이 maximum load 시간대의 전기요금보다 비교적 저렴한 light load, intermediate load 시간대에 pre-cooling을 하여 전기요금을 절감시키는 목적이며, 이는 Fig. 6의 cooling energy 그래프에서 각 제어방식마다의 cooling energy 사용량으로 보여준다.
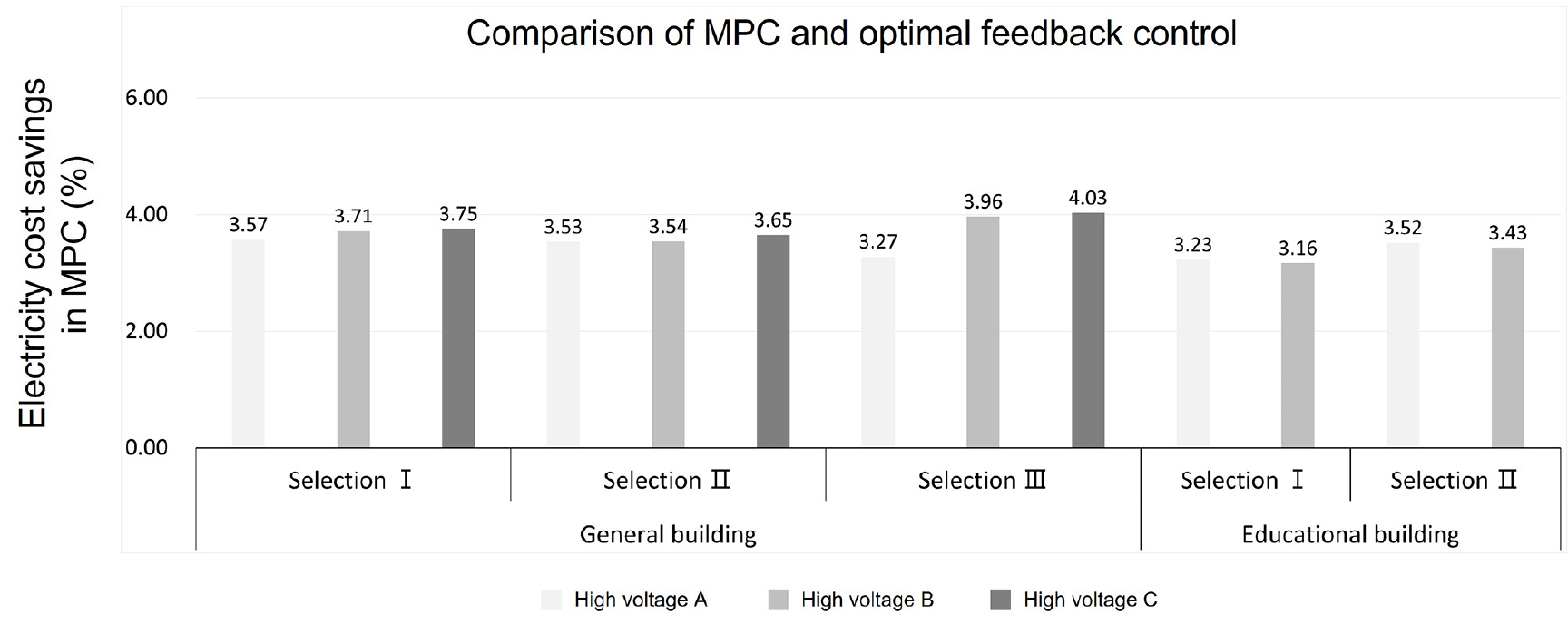
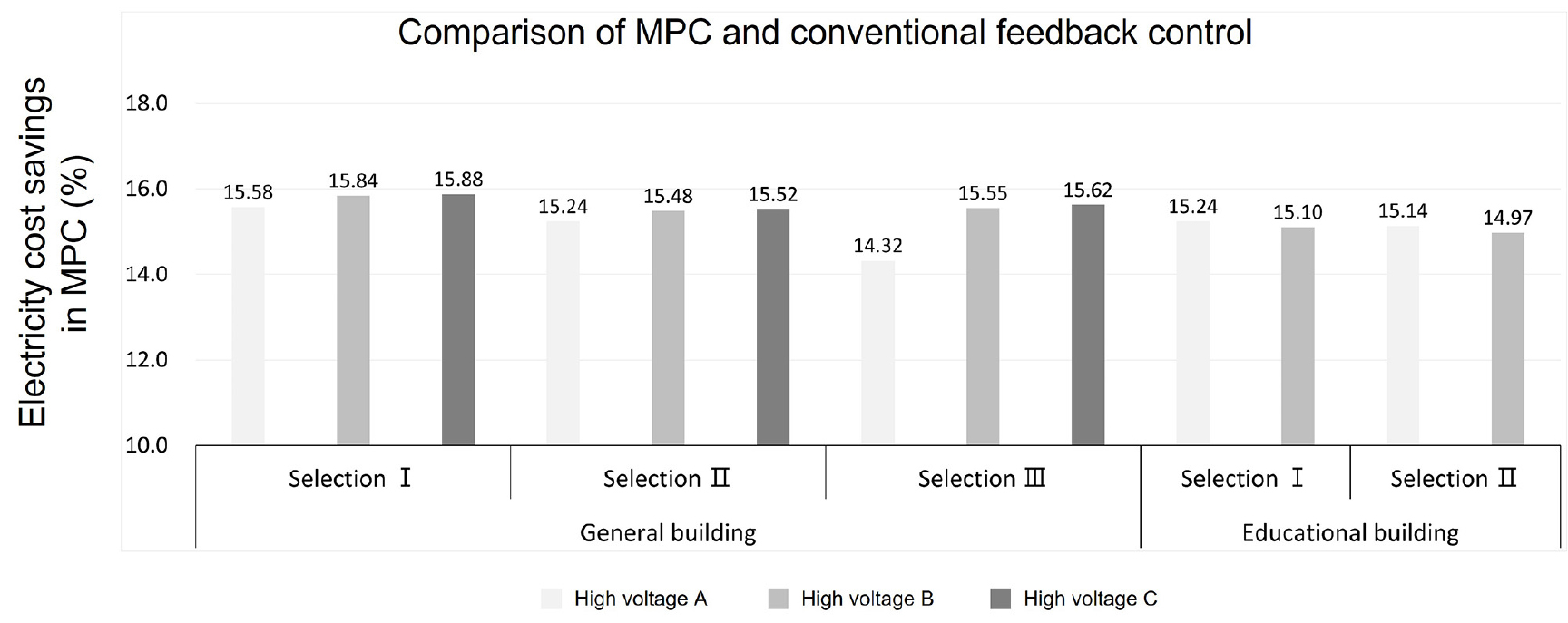
Figs. 7과 8은 전기비용 구조별 전기비용 절감량을 나타낸다. Fig. 7은 가장 최적의 되먹임 제어와 비교한 MPC에서의 전기비용 절감량이며 3.16 ~ 4.03%의 절감량을 보여준다. Fig. 8은 전력에 일정 계수를 곱한 일반적인 되먹임 제어와 비교한 MPC에서의 전기비용 절감량를 나타낸 것이며 14.32 ~ 15.88%의 절감량을 보여준다. MPC 시뮬레이션 결과 최적의 feedback과 비교해도 전기비용 절감이 이루어진다는 것과 최적의 feedback이 아닌 경우에 더욱 전기비용이 크게 절감된다는 것을 알 수 있다. 또한 본 연구에서의 대상 건물은 일반용 전기구조에서는 고압으로 갈수록 전기비용 절감량이 증가하고, 교육용 전기구조에서는 저압으로 갈수록 전기비용 절감량이 증가한다는 것을 볼 수 있다.
5. 결 론
본 연구는 실측 데이터에 기반하여 교육시설 건물을 대상으로 grey-box 모델링을 수행하였다. 주변 환경에 따라 변화하는 파라미터를 추가한 grey-box 모델과 추가하지 않은 모델의 비교를 통해서 추가하지 않은 모델(즉, LTI 모델)의 예측성능 정확성을 도출하였다. 이를 바탕으로 LTI 모델을 사용하여 MPC 시뮬레이션을 수행하였다. 다양한 국내 전기비용 구조를 MPC 시뮬레이션에 적용하여 정량적으로 분석하였으며 결과는 아래와 같이 정리된다.
(1) Grey-box 모델링 결과는 case1 ~ 3 모두에서 RMSE 1℃ 미만의 준수한 예측결과를 보여주었다.
(2) LTI 모델로 전기비용 감소를 목적으로 MPC 시뮬레이션을 수행한 결과 일반용, 교육용 건물에서 optimal feedback 제어와 비교하여 약 3.16 ~ 4.03% 전기비용 절감량을 보여주었다. 반면 conventional feedback 제어와 비교하여 약 14.42 ~ 15.88%의 절감량을 나타내었다.
위 결과로 MPC 시뮬레이션의 전기비용이 가장 이상적인 되먹임 제어와 비교하여도 3.16 ~ 4.03%의 절감량을 보여주는 것으로 보아 각 건물의 냉난방 운영 비용을 절감하는데 있어서 큰 역할을 할 것으로 기대된다. 또한 건물의 에너지 사용 시점을 On-peak에서 Off-peak로 옮김으로써 전기 사용의 피크를 줄이고 전기 에너지 관리의 안정성을 더하며 나아가 플랜트 설비의 용량을 낮춤으로써 탄소중립의 실현에 기여할 것으로 사료된다.
6. 향후 연구 과제
본 연구에서 전기비용만을 목적함수로 설정하여 MPC 시뮬레이션을 수행하였다. 하지만 국가 에너지 절감 및 국제적인 CO2 절감의 추세에서 전기 비용뿐 아니라 에너지 사용량 역시 줄이는 것이 필요하다. 따라서 향후 연구로써 건물군의 에너지 절감을 위한 연구를 수행할 예정이다. 이를 위하여 상세한 냉난방 시스템의 성능곡선이 요구된다. 또한 목적함수의 설정에 따른 전기에너지 및 비용 절감이 달라질 것으로 예상되며 이를 정량적으로 분석할 예정이다.
또한 단일 존을 이용한 MPC의 결과를 논의한 본 연구는 추후 분산 최적화를 적용하여 건물 전체의 MPC로 확장될 것이다. 이를 통해 실제 건물에 MPC를 적용하기 위한 적용성 및 일반화의 문제를 해결하는데 중점을 둘 것이다.