Estimation of Variability in Internal Rate of Return for Korea Offshore Wind Projects with Financing Conditions

Keon-Woo Lee; Kyung-Nam Ko

doi:10.7836/kses.2025.45.1.077

Preview

Research Article

Journal of the Korean Solar Energy Society. 28 February 2025. 77-89
https://doi.org/10.7836/kses.2025.45.1.077

Estimation of Variability in Internal Rate of Return for Korea Offshore Wind Projects with Financing Conditions

국내 해상풍력사업의 프로젝트 파이낸싱 조건에 따른 내부수익률 변동성 추정

Keon-Woo Lee¹

Kyung-Nam Ko²^*

이 건우¹

고 경남²^*

¹Ph. D. Candidate, Multidisciplinary Graduate School Program for Wind Energy, Graduate School, Jeju National University

²Professor, Department of Electrical and Energy Engineering, Jeju National University

¹제주대학교 대학원 풍력특성화협동과정, 박사과정

²제주대학교 전기에너지공학과, 교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution NonCommercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

An investigation into the variation in revenue based on project financing conditions was conducted for 20 offshore wind projects in Korea permitted by the government. Capital Expenditures (CapExs) and Operational Expenditures (OpExs) for these projects were estimated using data from a government commission and a report by the U.S. National Renewable Energy Laboratory. Wind speed distribution estimates for Korean territorial waters were used to calculate the annual energy production (AEP), leading to the determination of the capacity factor (CF), assuming the installation of 18 reference 15 MW wind turbines from the International Energy Agency (IEA) at the 20 project sites. Next, financial assumptions were established to compute the Internal Rate of Return (IRR), considering interest rates of 4.5%, 5.5%, and 6.5%, loan periods of 12, 15, and 18 years, and debt levels of 50%, 60%, 70%, 80%, and 90%. The results showed that equity IRR increased with a higher percent of debt, but the variability in IRR also grew, indicating higher financial risk. As the loan period lengthened, interest payments increased, leading to a reduction in taxes for the projects.

Keywords

Wind energy

Engineering economy

Percent of debt

IRR

Offshore wind energy

키워드

풍력에너지

경제성공학

타인자본 비율

내부수익률

해상풍력

MAIN

1. 서 론
2. 연구방법
2.1 연간발전량의 계산 방법
2.2 경제성공학 이론
2.3 분석대상 선정
2.4 전력판매가격의 산정
2.5 풍력발전기의 선정
3. 분석결과
3.1 연간발전량(AEP)과 이용률(CF) 산출
3.2 경제성 분석 가정
3.3 타인자본 비율, 대출기간 그리고 이자율의 변동에 따른 IRR 계산 결과
4. 결 론

1. 서 론

풍력발전, 태양광발전 등 재생에너지 발전 사업을 개발함에 있어 가장 중요한 요소는 프로젝트의 사업성이다. 최소 수 백억원의 막대한 금액이 투입 되는 프로젝트 개발의 사업성을 판단하기 위해서는 재무적 타당성을 평가해야한다. 재무적 타당성은 프로젝트 계획 기간의 편익과 비용을 분석하고 순현재가치(Net present value, NPV), 내부수익률(Internal rate of return, IRR), 회수기간(Payback period), 비용-편익비율(Benefit-Cost Ratio, BCR) 등 다양한 경제성 지표들을 활용하여 평가한다¹⁾.

2023년 말까지 전기위원회의 발전사업허가를 획득한 국내 해상풍력발전단지는 84개소 약 27 GW이며 이들 중 52개소 약 15.6 GW가 전라남도에 위치하고 있다²⁾. 전기위원회의 발전사업허가를 받은 프로젝트 중, 전기위원회의 회의록에서 확인되는 해상풍력발전 프로젝트의 예상 용량과 사업비의 평균은 각각 약 335 MW와 약 1.8조원이고 예상 사업비에서의 타인자본 비율은 최소 70% ~ 최대 90%로 다양하게 제시되어 있다³⁾. 또한 서남해 해상풍력 실증단지의 타인자본 비율은 50%이다⁴⁾.

풍력발전사업 개발 프로젝트에서 자금 조달을 위해 주로 이용되는 프로젝트 파이낸싱(Project Financing, PF) 방식은 특정 사업의 수익을 통해 투자금을 회수하는 구조로, 투자자 자산과 사업 자산을 분리하고 신용위험을 최소화하기 위해 독립적인 특수목적법인(Special purpose company, SPC)을 설립하여 사업을 진행하는 것이 일반적이다. SPC는 사업에서 발생하는 위험을 효과적으로 분리하여 관리할 수 있을 뿐만 아니라, 자산 및 부채를 체계적으로 관리할 수 있는 장점을 제공한다⁵⁾. 즉, 서남해 해상풍력 실증단지의 사례와 같이 해상풍력 프로젝트는 투자위험부담을 줄이기 위하여 사업추진주체가 한 기업이 아닌 다양한 기업이 합작하여 SPC를 설립한 후 사업 개발을 추진한다.

SPC는 사업 현금흐름을 담보로 대규모 투자금을 조달하며, 자본금을 최소화하는 동시에 차입금을 활용한 레버리지를 통해 투자수익률(Return on equity, ROE), 즉 자기자본 투자자의 내부수익률(IRR) 극대화를 도모한다⁶⁾. 투자자는 적절한 자기자본 비율과 타인자본 비율을 설정함으로써 투자 수익을 극대화하는 동시에 프로젝트의 재무적 안정성을 확보할 필요가 있다. 이러한 균형 잡힌 접근은 SPC 구조의 장점을 최대한 활용하는 데 중요한 요소로 작용한다. 따라서 총 투자비 규모, 대출 이자율, 대출기간 등을 고려하여 적절한 자기자본 비율을 설정해야 하며, 동시에 수익의 극대화를 추구하기 위해 이자율, 대출기간, 타인자본 비율의 변동에 따른 수익률(IRR)의 변동성을 분석할 필요성이 있다.

최근 국내에서는 고정식 해상풍력발전 단지의 LCOE 연구^7,8), 부유식 해상풍력발전단지의 LCOE 연구⁹⁾ 등 해상풍력발전단지의 발전원가에 관한 연구가 주로 수행되고 있으며 이는 실제 해상풍력 프로젝트 개발에 수행되는 경제성 분석과는 조금 차이가 있다. 경제성 분석에서는 풍력발전단지의 수익, 비용, 세금 그리고 대출 등 다양한 요소가 고려되며 이로부터 사업성을 분석한다. 발전원가에 관한 연구는 풍력발전단지의 수익과 비용에 관한 요소들은 고려하지만 세금, 대출 등에 관한 요소들은 고려되지 않으므로 이에 대한 연구가 필요하다. 이러한 연구는 신규 해상풍력 프로젝트를 기획하고 있는 사업자들에게 타인자본 비율, 이자율, 대출기간에 따른 세금과 수익성의 기본적인 변동성에 관한 정보를 제공하여 프로젝트 파이낸싱에 관한 의사결정에 도움을 줄 수 있을 것이다.

본 연구에서는 이자율, 대출기간, 타인자본 비율의 변동에 따른 IRR의 변동성을 분석하고자 한다. 먼저, 국내 해상풍력발전 개발 프로젝트의 총 투자비(Capital expenditure, CapEx) 데이터를 수집하고 연간운영비용(Operational expenditure, OpEx)을 산정한다. 그리고 한국 영해의 풍속 분포 추정값을 이용하여 연간발전량(Annual energy production, AEP)과 이용률(Capacity factor, CF)을 계산한다. 그 다음, 이를 활용하여 다양한 타인자본 비율, 대출기간, 대출 이자율의 조합을 경제성 분석에 적용하여 이들의 변동에 따른 IRR의 변동성을 분석하였다.

2. 연구방법

2.1 연간발전량의 계산 방법

측정된 바람데이터가 없으므로 바람자원지도의 와이블(Weibull) A와 K 계수를 이용하여 총 연간발전량(Gross AEP, $A E P_{G r o s s}$ ), 순 AEP (Net AEP, $A E P_{N e t}$ )와 순 이용률(Net CF, $C F_{N e t}$ )를 계산하였고 총 AEP 계산식은 아래와 같다¹⁰⁾.

(1)

A E P_{G r o s s} [k W h] = N_{h} \int_{v_{c u t - i n}}^{v_{c u t - o u t}} f (v) P (v) d v \approx N_{h} \sum_{i = 1}^{n} (F (v_{i}) - F (v_{i - 1})) (\frac{P_{i} - P_{i - 1}}{2})

여기서, $N_{h}$ 는 1년의 시간의 수(8,760 시간)이고, $v_{c u t - i n}$ 은 풍력발전기의 시동 풍속, $v_{c u t - o u t}$ 은 풍력발전기의 종단 풍속, $f (v)$ 는 와이블 분포의 확률밀도함수, $P (v)$ 는 풍속에 대한 풍력발전기의 출력이고 $v$ 와 $v_{i}$ 는 풍속과 i 번째 풍속이다. $F (v_{i})$ 와 $F (v_{i - 1})$ 는 각각 i 번째 풍속과 i -1번째 풍속에 대한 와이블 분포의 누적분포함수, $P_{i}$ 와 $P_{i - 1}$ 는 각각 i 번째 풍속과 i -1번째 풍속에 대한 풍력발전기의 출력이다.

순 AEP와 순 CF은 각각 식(2) ~ 식(3)과 같다^11,12).

(2)

N e t A E P [k W h] = A E P_{G r o s s} - δ \times A E P_{G r o s s}

(3)

C F_{N e t} [%] = \frac{A E P_{N e t}}{N_{h} \times P_{r a t e d}} \times 100

여기서, $δ$ 는 후류손실, 풍력발전기 성능에 대한 손실, 송전 손실, 환경요인에 의한 손실 등을 고려한 총 AEP 손실률이고. $P_{r a t e d}$ 는 풍력발전기의 정격 출력이다.

2.2 경제성공학 이론

타인자본 비율, 이자율 그리고 대출기간의 변동만을 고려하여 사업성을 분석하고 이들이 IRR에 미치는 영향을 확인하기 위하여 경제성공학의 분석 방법 중 부채를 고려한 세후경제성분석 방법¹³⁾을 사용하였다. 하지만 다른 변수들의 영향을 배제하고 이들의 영향만을 분석하기 위하여 총 투자비, 풍력발전단지의 수익, 풍력발전단지의 연간운영비용, 물가상승률, 감가상각(Depreciation), 원리금균등분할상환방법, 세금(Tax)을 고려하였다.

IRR은 수익의 현금흐름을 현재가치로 환산하여 합한 값이 투자지출과 같아지도록 하는 이자율이다¹⁴⁾. 즉, NPV를 0으로 만드는 이자율이며 계산식은 다음 식(4)와 같다.

(4)

N P V = \sum_{i = 1}^{N} \frac{A T C F_{i}}{(1 + I R R)^{i}} = 0

여기서, $A T C F_{i}$ 는 i년의 세후현금흐름이다.

부채를 고려하지 않은 프로젝트의 세후현금흐름( $A T C F_{P r o j e c t}$ ), 즉 100% 자기자본 총투자의 세후현금흐름은 다음과 같이 계산된다.

(5)

A T C F_{P r o j e c t} = I n c o m e_{t a x a b l e} - T a x + D e p r e c i a t i o n

여기서, $I n c o m e_{t a x a b l e}$ 은 과세대상소득이고 다음과 같이 계산된다.

(6)

I n c o m e_{t a x a b l e} = R e v e n u e - O p E x - D e p r e c i a t i o n

부채를 고려한 자기자본(Equity)의 세후현금흐름( $A T C F_{E q u i t y}$ )은 다음과 같이 계산된다.

(7)

A T C F_{E q u i t y} = I n c o m e_{t a x a b l e, E q u i t y} - T a x - R e p a y m e n t_{P r i n c i p a l} + D e p r e c i a t i o n

여기서, $I n c o m e_{t a x a b l e, E q u i t y}$ 는 자기자본의 과세대상소득, $D e p r e c i a t i o n$ 은 매년 감가상각비로, 고정자산에 대하여 정액법으로 계산된 금액이다. $R e p a y m e n t_{P r i n c i p a l}$ 은 원리금균등분할상환방법의 상환원금이다.

자기자본의 과세대상소득은 다음과 같이 계산된다.

(8)

I n c o m e_{t a x a b l e, E q u i t y} = R e v e n u e - O p E x - D e p r e c i a t i o n - I n t e r e s t

여기서, $I n t e r e s t$ 는 원리금균등분할상환방법의 이자상환액이다.

2.3 분석대상 선정

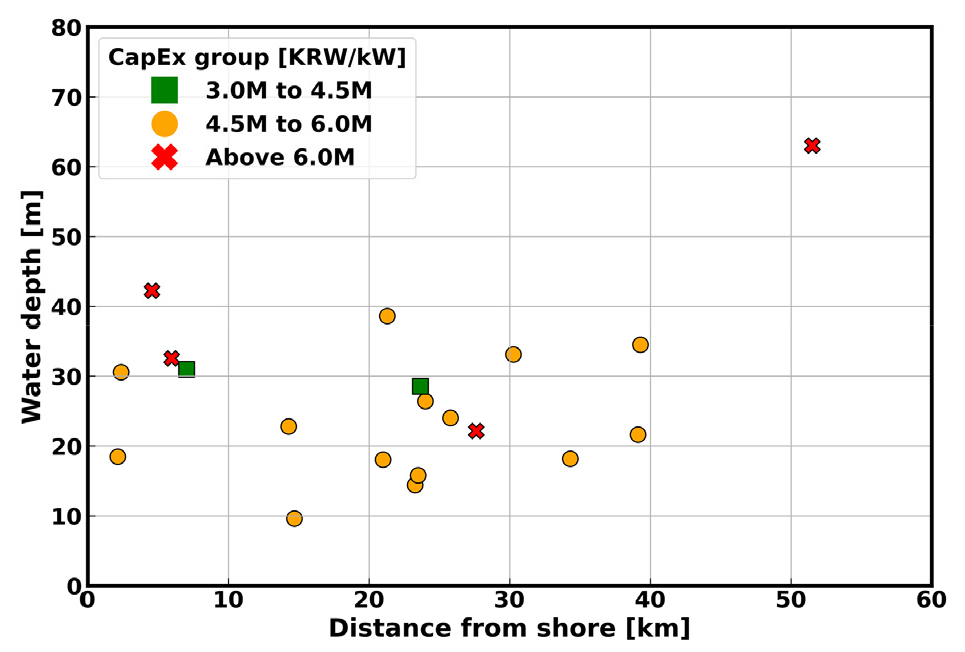
Table 1은 분석을 위하여 선정된 고정식 해상풍력발전단지의 CapEx, 발전단지의 설비용량, CapEx 대비 OpEx 비율, CapEx 보정 계수, 수심 그리고 해안선으로부터의 거리를 나타낸다. 해상풍력발전단지는 전기위원회의 발전사업허가를 받은 곳 중 발전단지의 설비용량뿐만 아니라 풍력발전기의 설치 기수, 타인자본 비율 그리고 예측 CapEx가 전기위원회에 제시된 20 개소를 선정하여 분석하였다. 20개소의 총 설비용량은 약 267.43 MW이며 이들의 kW 당 예측 CapEx는 5,314,017원이었다. OpEx는 NREL의 2024년 보고서¹⁵⁾에 보고된 2023년 고정식 해상풍력의 CapEx와 OpEx를 사용하여 CapEx 대비 OpEx 비율을 계산하여 사용하였고 이는 2.49%였다. CapEx 보정계수는 NREL의 2023년 보고서¹⁶⁾에 보고된 2022년 CapEx와 2024년에 보고된 2025년 CapEx 예측치¹⁷⁾를 이용하여 증가율 47.13%를 활용한 것으로 1.4713이다. 이는 2022년 CapEx 4,640 USD/kW와 2025년 6,000 USD/kW에 2022년 평균 환율 1,291.95원과 2024년 12월 말일 환율 1,470.00원을 적용한 후 계산한 결과이다. 최근 공급망 전반의 인플레이션으로 인하여 풍력발전기의 원자재가격, 공사비 등이 상승하고 있고 이에 따라 CapEx 또한 증가하는 추세이다¹⁸⁾. 선정된 해상풍력발전단지의 CapEx는 인플레이션의 영향이 반영되지 않은 수치이므로 이를 반영하기 위하여 보정계수를 적용하였다.

수심은 해양조사원의 자연과학용 수심 데이터¹⁹⁾를 활용하여 도출하였다. 이 데이터는 해양조사원에서 수심측량자료를 기반으로 만든 수치모델을 위한 해양수치모델 전용 수심 데이터세트로 150 m의 해상도를 가지고 있다. 계산 결과, 20개소의 평균 수심은 약 21.79 m였다. 해안선으로부터의 거리는 사이트로부터 가장 가까운 본토의 해안선까지의 거리이며 평균 27.62 km로 나타났다. 평균 수심과 평균 해안선으로부터의 거리는 REC 가중치를 계산하는데 사용되었다.

Table 1.

Summary for Korean offshore wind farm and NREL data

Items	No. of data	Mean	SD
CapEx [KRW/kW]	20	5,314,017	797,436
Total capacity of wind farm [MW]	20	267.43	134.79
The ratio of CapEx to OpEx [%]	1	2.49	-
CapEx correction factor [-]	1	1.4713	-
Water depth [m]	20	21.79	13.07
Distance from shore [km]	20	27.62	12.76

Fig. 1은 Table 1에 나타낸 20개소의 고정식 해상풍력발전단지의 CapEx, 해안선으로부터의 거리 그리고 수심을 나타낸다. 단위 용량 당 CapEx는 대부분 4,500,000원/kW부터 6,000,000원/kW에 형성되어 있다. 선정된 20개소의 수심은 최대 63 m까지 형성되어 있으며 고정식 해상풍력의 하부구조물 중 자켓(Jacket) 형식은 설치 수심이 최대 100 m까지 가능하다²⁰⁾.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F1.jpg

Fig. 1.

CapEx in accordance with distance from shore and water depth

2.4 전력판매가격의 산정

IRR 계산에 필요한 풍력발전단지의 수익을 계산하기 위해서는 연간발전량과 전력판매가격인 SMP와 REC 데이터가 필요하다²¹⁾. SMP와 REC 정보는 2024년 풍력 고정가격계약 경쟁입찰의 상한가격²²⁾을 이용하였다. 해상풍력의 SMP + 1REC는 176,565원/MWh였고 기준 전력거래가격은 86,350원/MWh이므로 REC는 90,215원/MWh이다. 해상풍력의 REC 기본 가중치는 2.5이며 복합가중치는 연계거리와 수심에 따라 선형적으로 증가하므로 Table 1의 수심과 해안선으로부터의 거리의 평균값을 적용하여 복합가중치의 평균을 산출하였고 그 값은 3.47이다. 따라서 본 연구에서는 해상풍력발전단지의 수익 계산에 SMP + 3.47REC를 적용하였다.

2.5 풍력발전기의 선정

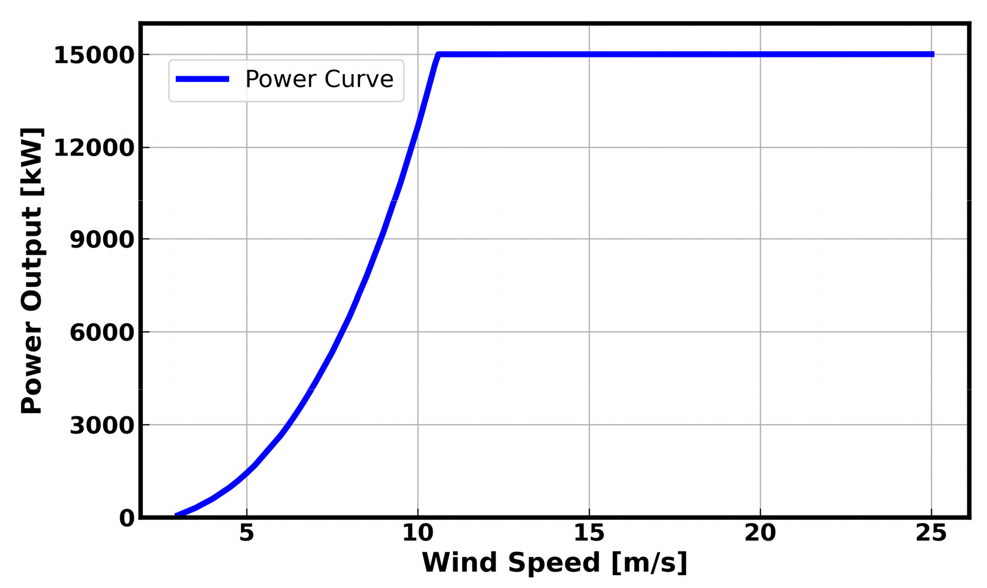
AEP 계산을 위하여 풍력발전기를 선정하여야 한다. 본 연구에서는 국제에너지기구(International energy agency, IEA)의 reference 15 MW 풍력발전기²³⁾를 사용하였다. 허브높이와 로터직경은 각각 150 m와 240 m이며 정격 풍속은 10.6 m/s이다. 아래의 Fig. 2는 IEA reference 15 MW 풍력발전기의 출력 곡선을 나타낸다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F2.jpg

Fig. 2.

Power curve of IEA 15 MW wind turbine

3. 분석결과

3.1 연간발전량(AEP)과 이용률(CF) 산출

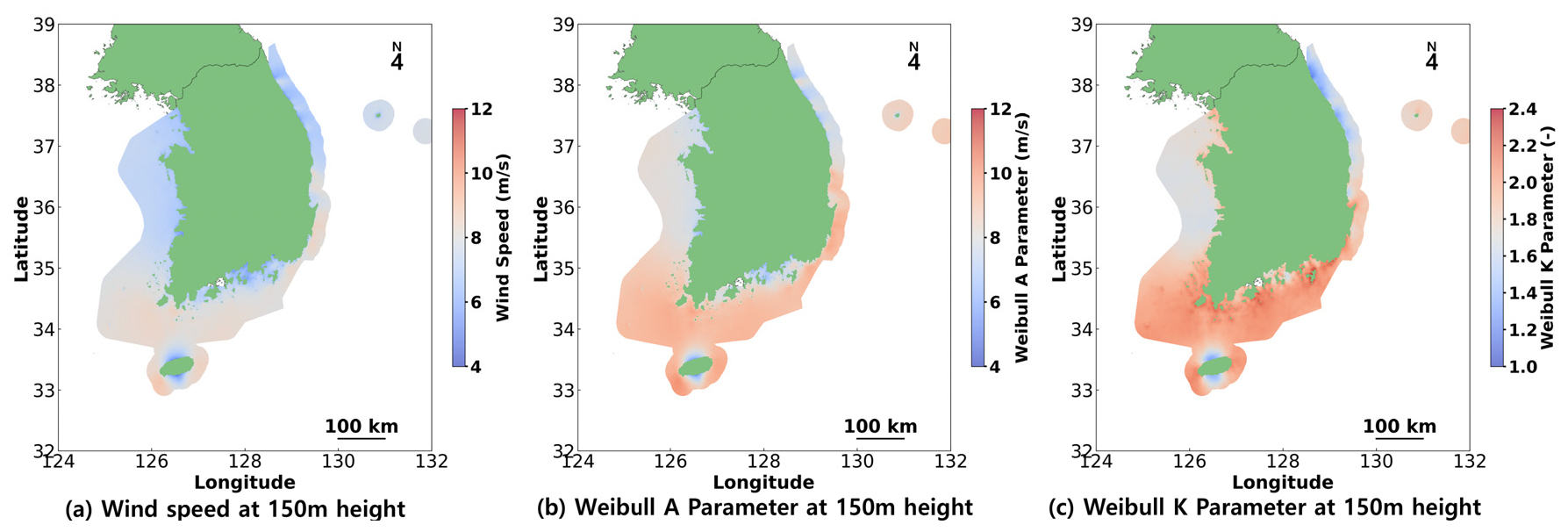
2.1절과 2.5절을 활용하여 AEP를 산출하였다. AEP를 산출하기 위해서는 와이블 분포의 계수가 필요하지만 측정된 바람 데이터가 없으므로 바람자원지도 데이터를 활용하였다. 바람자원지도는 DTU (Technical university of Denmark)와 EMD international A/S에서 제작한 GASP (the Global Atlas for Siting Parameters) 데이터²⁴⁾를 사용하였다. Fig. 3은 우리나라 영해 내에 위치한 GASP 데이터의 150 m 풍속, 와이블 A 계수 그리고 와이블 K 계수를 보여준다. 각 데이터 포인트의 수는 1,233,925개이며 포인트 격자의 해상도는 250 m이다. 150 m 풍속, 와이블 A 계수 그리고 와이블 K 계수의 평균은 각각 7.68 m/s, 8.64 m/s 그리고 1.87로 나타났다. 이 값들은 본 연구목적을 위하여 검증없이 그대로 사용하였으므로 실제값과는 차이가 날 수 있다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F3.jpg

Fig. 3.

Wind speeds, Weibull A and K parameters at 150 m height from GASP

Table 1에서 풍력발전단지 용량 평균이 약 267 MW이므로 15 MW 풍력발전기 18기, 총 270 MW 설비용량을 가진 가상의 해상풍력발전단지를 구성하여 분석을 수행하였다. 또한 분석에 사용되는 연AEP와 CF가 대표성을 갖도록 와이블 A와 K 계수의 평균값을 AEP 계산에 사용하였고 계산 결과, 총 AEP는 약 1,044,279,141 kWh였다. 순 AEP와 순 CF를 계산하기 위하여 AEP 에 대한 총 AEP 손실을 산정해야한다. 총 손실은 NREL의 2024년 보고서¹²⁾에서 제시된 고정식 해상풍력의 손실인 15.5%를 적용하였고 계산결과 순 AEP와 순 CF는 각각 882,415,874 kWh와 37.31%였다.

이 계산 결과는 AEP에 총 손실을 고려한 계산결과이며 P50 AEP와 CF에 해당하는 결과이다. 풍력발전사업의 경제성 분석 시, 주로 P75의 AEP와 CF가 사용된다. P75를 계산하기 위해서는 P50 계산결과와 20년 평균 불확도가 필요하며 본 연구에서는 불확도를 10.0%로 가정하였다. 이때 P50 계산결과는 중심 추정치의 역할을 하고 불확도는 편차의 역할을 한다. P75 AEP는 해당 AEP를 초과할 확률이 75%라는 것을 의미한다. P50 계산결과에 20년 평균 불확도를 적용하여 P75 순 CF를 계산한 결과 34.79%였고 이를 활용하여 경제성 분석을 실시하였다.

3.2 경제성 분석 가정

Table 2는 IRR 계산을 위한 경제성 분석의 가정을 나타낸다. 가상의 해상풍력발전단지의 kW 당 CapEx는 7,818,513원으로 MW 당 약 78억 원이었고 OpEx는 194,681원/kW-yr였다. 이때, kW 당 CapEx는 Table 1의 CapEx와 CapEx 보정계수 1.4714을 곱한 값이다. SMP, REC 그리고 REC 가중치는 2.4절에 나타내었고 물가상승률은 2.00%를 적용하였다. 감가상각 기간과 발전단지 운영기간은 모두 20년으로 가정하였고 P50 CF와 P75 CF는 3.1절에 나타내었다. 운영기간을 20년으로 가정한 것은 풍력 고정가격계약 기간이 20년이기 때문이다. 타인자본 비율(Gearing, % of debt), 대출기간(Loan period) 그리고 대출 이자율(Interest rate)의 변동에 따른 IRR 분석을 위하여 다음과 같이 가정하였다. 서남해 해상풍력 개발사업의 타인자본 비율이 50%⁴⁾이고 전기위원회에 제출된 해상풍력발전단지들의 사업계획³⁾ 중 타인자본의 비율이 최대 90%까지 보고되었으므로 타인자본 비율은 50%, 60%, 70%, 80% 그리고 90%를 가정하였다. 대출기간과 대출 이자율은 각각 12년, 15년, 18년과 4.5%, 5.5%, 6.5%를 가정하여 경제성 분석을 실시하고 IRR의 변동을 분석하였다.

Table 2.

Analysis assumption

Items	Value
CapEx [KRW/kW]	7,818,513
OpEx [KRW/kW-yr]	194,681
Total capacity of wind farm [MW]	270
Inflation rate [%]	2.00
Interest rate [%]	4.5, 5.5, 6.5
Loan period [yr]	12, 15, 18
Depreciation period / Operation period [yr]	20 / 20
Gearing (% of debt) [%]	50, 60, 70, 80, 90

3.3 타인자본 비율, 대출기간 그리고 이자율의 변동에 따른 IRR 계산 결과

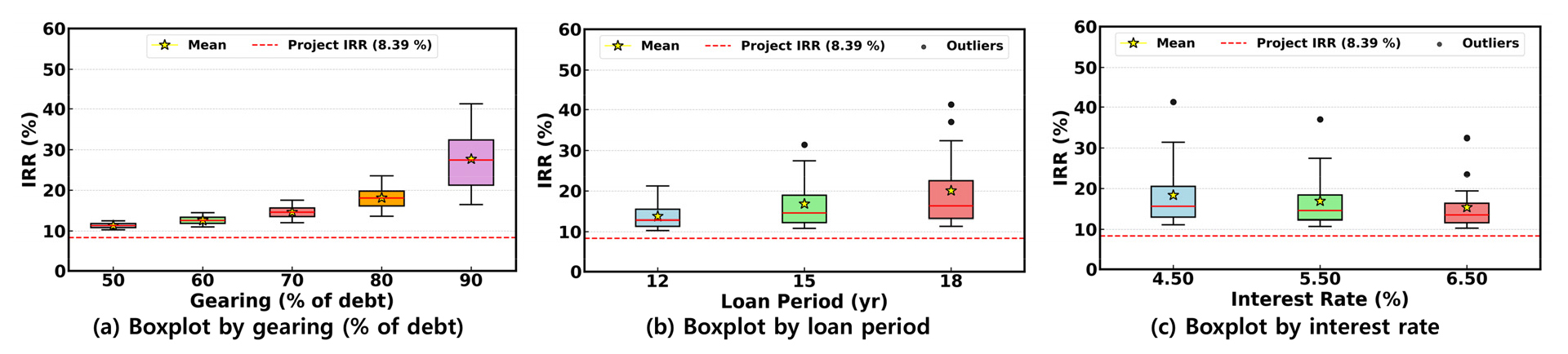
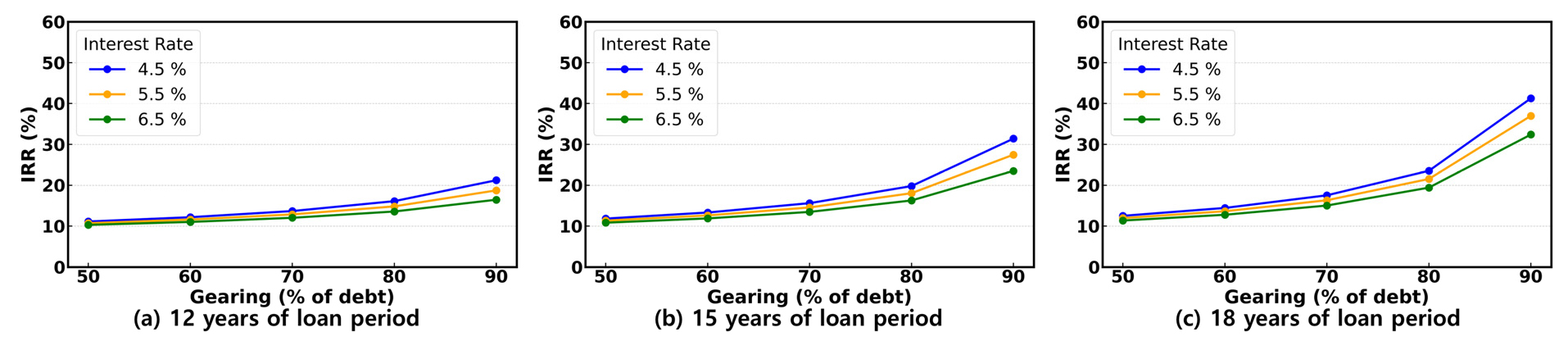
Fig. 4는 타인자본 비율, 대출기간 그리고 대출 이자율의 변동에 따른 자기자본의 IRR 산출 결과를 상자그림(Boxplot)으로 나타낸다. 총투자, 즉 프로젝트의 IRR (Project IRR)은 8.39%로 대출 이자율의 최댓값인 6.5%보다 높으므로 경제성이 있는 것으로 나타났고, 자기자본의 IRR (Equity IRR)은 모두 프로젝트의 IRR보다 높았다. 하지만 이 결과는 실제값이 아닌 가정과 단순화된 수식에 의해 도출된 결과이므로 실제값과 차이가 있을 수 있다. Fig. 4(a)는 IRR과 타인자본 비율에 대한 상자그림이다. 타인자본 비율 50%, 60%, 70%, 80% 90%에서 IRR의 중앙값은 각각 11.34%, 13.32%, 15.61%, 19.79%, 32.40%였다. IRR의 최솟값은 타인자본 비율 50%에서 10.3%, IRR의 최댓값은 타인자본 비율 90%에서 41.26%로 나타났다. 또한 타인자본 비율이 커질수록 변동성이 지수적으로 커지면서 IRR이 극대화되는 것을 확인할 수 있었고 이상치(Outlier)는 없었다.

Fig. 4(b)는 IRR과 대출기간에 대한 상자그림이다. 대출기간 12년, 15년 18년의 중앙값은 12.86%, 14.56%, 16.32%로 비슷하였으나 이상치를 제외한 상자그림의 최댓값은 21.61%, 28.93%, 36.53%로 약 7% 씩 차이가 있었다. 상자그림의 최댓값과 최솟값은 이상치를 제외한 데이터의 최대와 최소 범위를 표현하는 수염(Whisker)부분이며 3사분위수(3Q)와 1사분위수(1Q)의 차이인 IQR (Interquartile range)의 1.5배 범위 안에 위치하고 있다. 이상치는 15년에서는 타인자본 비율 90%와 대출 이자율 4.5%에서, 18년에서는 타인자본 비율 90%와 대출 이자율 4.5%, 5.5%에서 나타났다. 이는 대출기간이 18년일 때 타인자본 비율과 대출 이자율의 조건에 따라 IRR이 극대화될 수 있음을 보여준다.

Fig. 4(c)는 IRR과 대출 이자율에 대한 상자그림이다. 대출 이자율 4.5%, 5.5% 6.5%의 중앙값은 15.61%, 14.56%, 13.47%로 비슷하였으나 최댓값은 31.89%, 27.57%, 23.47%로 약 4% 씩 차이가 있었고 모든 이상치는 모두 타인자본 비율 90%에서 나타났다. 대출기간 18년과 타인자본 비율 90% 조합은 모두 이상치였고 대출 이자율 5.5%와 6.5%에서는 대출 기간 15년과 타인자본 비율 90% 조합도 이상치로 판정되었다. 이 상자그림의 결과는 이자율이 낮을수록 IRR이 극대화됨을 보여준다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F4.jpg

Fig. 4.

Boxplot by gearing (a), loan period (b) and interest rate (c)

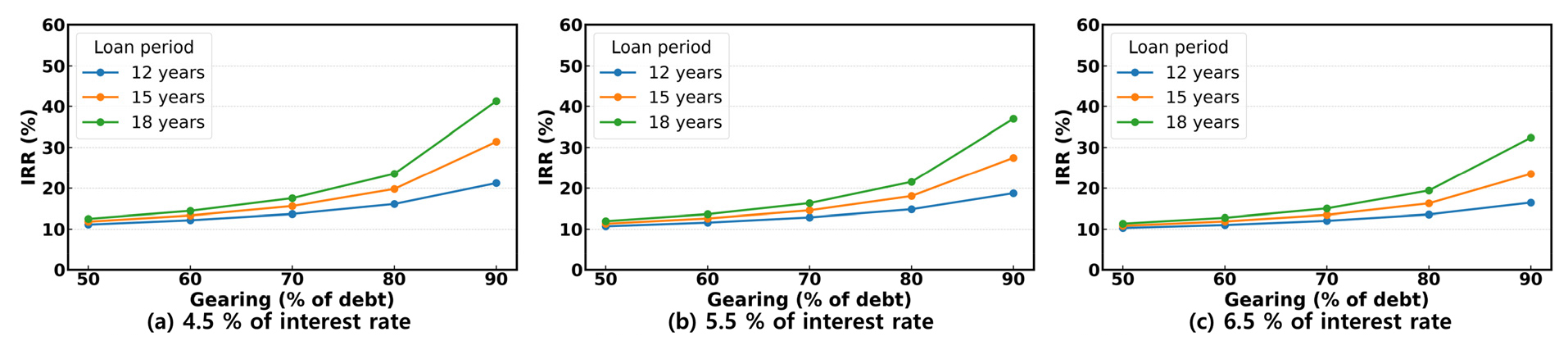
Fig. 5는 대출기간과 타인자본 비율에 따른 IRR의 추세를 보여준다. 대출기간이 길어질수록 타인자본 비율의 증가에 대한 IRR 상승폭이 점차 증가하고 있으며 이자율이 낮을수록 IRR 상승폭이 더 커지고 있다. 대출기간 12년의 이자율 4.5%에서 타인자본 비율 50%일 때 IRR과 타인자본 비율 90%일 때 IRR의 증가율을 계산하면 약 0.91배이다. 이자율 4.5%에서 타인자본 비율 50%에서 90%로의 증가율은 각각 대출기간 15년약 1.65배와 18년 약 2.30배로 대출기간이 길고 타인자본 비율이 높을 때 IRR이 극대화됨을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F5.jpg

Fig. 5.

Trends of IRR with gearing and loan periods

Fig. 6은 이자율과 타인자본 비율에 따른 IRR의 추세를 보여준다. 이자율이 높아질수록 타인자본 비율의 증가에 대한 IRR의 증가분이 점차 감소하고 있다. 이자율 4.5%의 대출기간 18년에서 타인자본 비율 50%일 때 IRR에서 타인자본 비율 90%일 때 IRR의 증가율은 약 2.30배이다. 그리고 이자율 5.5%와 6.5%의 대출기간 18년에서 타인자본 비율 50%에서 타인자본 비율 90%로의 증가율은 각각 약 2.09배와 약 1.85배로 이자율이 증가할수록 IRR이 감소함을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F6.jpg

Fig. 6.

Trends of IRR with gearing and interest rates

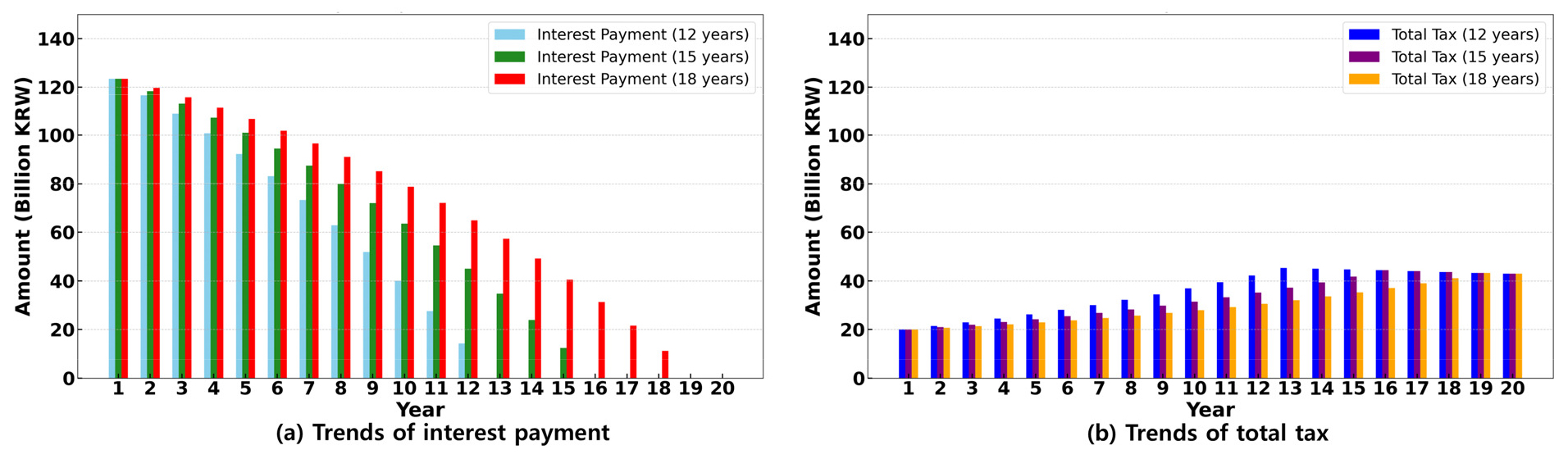
Fig. 7은 대출기간에 따른 운영 연차별 이자상환과 총 세금의 추세를 보여준다. 대출기간이 길어질수록 매년 상환하는 원금의 크기가 작아지므로 매년 지불해야하는 이자가 커진다. 대출 이자는 법인세에 대한 절세효과로 작용하여 대출기간이 길수록 법인세의 절세효과가 커진다. 그림에서도 이를 확인할 수 있으며 상환 이자의 크기와 법인세의 절세효과는 모두 12년, 15년, 18년 순으로 커짐을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F7.jpg

Fig. 7.

Trends of total tax and interest payment with loan periods over 20 years

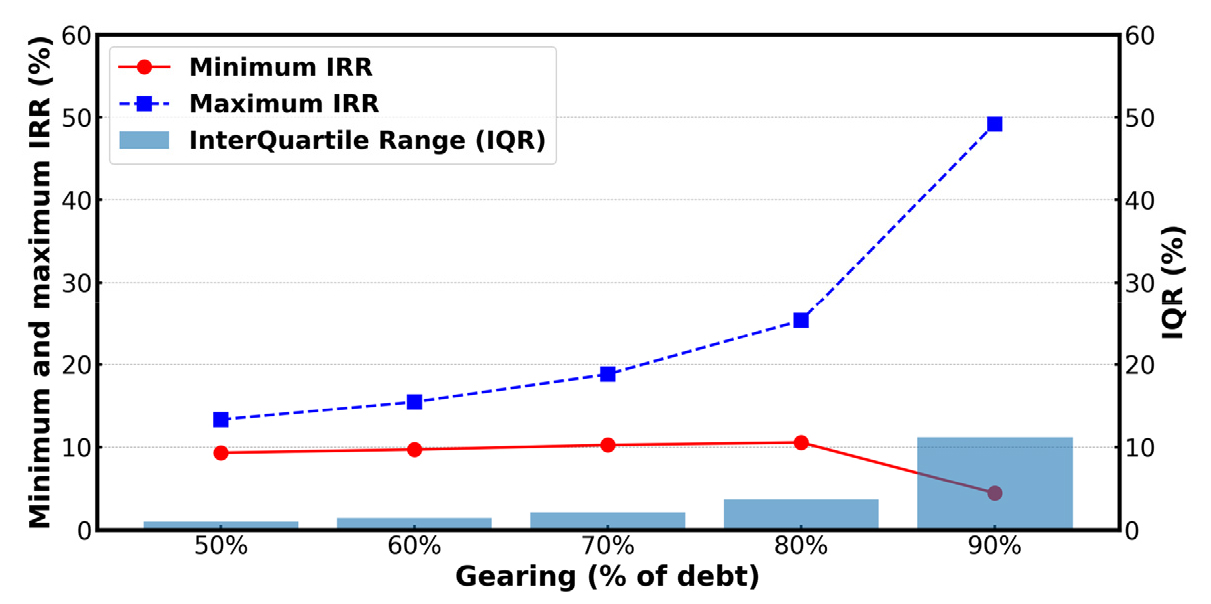
Fig. 8은 타인자본 비율이 IRR에 미치는 영향과 금융 리스크를 나타낼 수 있는 최솟값, 최댓값, IQR을 함께 보여준다. 최대 기대 수익률인 IRR의 최댓값은 타인자본 비율 50% ~ 80%까지 13.33%에서 25.33%로 12.00% 증가하였으나 80%에서 90%는 25.33%에서 49.17%로 23.84% 급등하였다. 그리고 타인자본 비율 50% ~ 80%까지 약 10%에서 유지되던 최소 기대 수익률, 즉 최솟값은 타인자본 비율 90%에서 4.45%로 급락하였다. 변동성을 보여주는 IQR은 타인자본 비율 50%에서 90%까지 지수적으로 증가하는 추세를 보이고 있으며 타인자본 비율 90%에서 급격히 증가하였다. 이는 타인자본 비율 90%에서 금융 리스크가 커지며 금융 안정성이 저하되고 있음을 보여준다.

https://cdn.apub.kr/journalsite/sites/kses/2025-045-01/N0600450107/images/kses_2025_451_77_F8.jpg

Fig. 8.

Impact of gearing on IRR with financial risk

4. 결 론

본 연구에서는 발전사업허가를 받은 국내 20개소의 고정식 해상풍력발전 프로젝트의 CapEx를 활용하여 타인자본 비율, 대출 이자율, 대출기간의 변동에 따른 내부수익률 분석을 수행하였다. 그 결과 다음과 같은 결론을 얻을 수 있었다. 단, 추정된 IRR값들은 개별 해상풍력발전단지들의 AEP의 실제값이 아닌 추정값을 이용하여 구하였으므로 실제 해상풍력발전단지의 IRR값과 다를 수 있음에 유의해야 하며 실제 해상풍력발전단지의 IRR을 분석하기 위해서는 반드시 개발 사이트에서 측정된 바람데이터와 적합한 금융조건을 사용하여야 한다.

•타인자본 비율이 증가할수록 레버리지효과로 인하여 IRR이 극대화되고 변동성이 커지며 대출기간이 길수록 IRR이 커짐을 확인하였다. 특히 타인자본 비율 90%에서 자기자본의 IRR의 최댓값과 중앙값은 각각 41.26%와 27.47%였다. 이로부터 자기자본을 최소화하고 타인자본의 비율을 높이는 자본 구조에서 IRR의 변동성이 커지면서 위험성이 증가하지만 IRR을 극대화할 수 있음을 확인하였다. 타인자본 비율 50%에서는 IRR의 최솟값과 최댓값이 각각 10.30%와 12.51%로 변동성이 작고 IRR이 낮지만 안정적으로 나타남을 확인하였다.

•대출기간 12년, 15년, 18년의 현금흐름을 비교한 결과, 대출기간이 길어질수록 매년 발생하는 이자의 상환액이 증가하였고 법인세의 절감 효과가 커지는 경향이 나타났다. 이는 대출조건 최적화를 통해 장기적인 프로젝트 경제성을 강화할 수 있음을 시사한다.

•대출 이자율이 높아질수록 IRR의 증가율이 감소함을 확인하였고 연구조건 하에서 이자율 변동에 대한 IRR의 변동률이 대출기간 변동에 의한 IRR의 변동률보다 작았다.

•타인자본 비율 90%에서는 이전 보다 IRR 변동성이 급격히 증가하여 금융 안정성이 저하되는 현상이 나타났다. 따라서 본 연구의 분석 조건 하에서는 금융 안정성을 위해서는 타인자본 비율 70%이하, 적절한 레버리지 효과를 누리기 위해서는 타인자본 비율 70% ~ 80%가 적절한 것으로 판단되며 90% 이상의 타인자본 비율에서는 금융 리스크가 급격히 증가할 가능성이 높으므로 신중한 판단이 필요하다. 그리고 대출기간과 대출이자율은 해상풍력발전단지 개발 부지의 환경과 다양한 금융 조건에 의해 신중히 결정되어야 한다.

Acknowledgements

이 논문은 2023년도 제주대학교 연구교수 기간에 연구되었음.

References

Kim, D,. Park, B., Lee, H., and Yun, J., A Study on the Interim Evaluation of the Financial Feasibility of Wind Power Plants in Operation, The 2023 Conference of The Korean Institute of Electrical Engineers, pp. 806-807, 2023, Jeju, Republic of Korea.

Korea Wind Energy Industry Association, 2023 Annual Report on Wind Energy Industry in Korea, KWEIA, Seoul, Republic of Korea, 2024.

Korea Electricity Regulatory Commission. https://www.korec.go.kr/. last accessed on the 8^th January 2025.

Korea Offshore Wind Power. http://www.kowp.co.kr/business/development03.asp. last accessed on the 8^th January 2025.

Kim, K., Yoon. T., Ahn, S., and Lee, C., A Seeking Improvement Plans and Criticism to Feasibility Study of Industrial Complex in Local Government: Focusing on Fiscal Impact and Financial Analysis with Various Approaches, The Korea Journal of Local Public Finance, Vol. 28, No. 2, pp. 155-184, 2023, https://doi. org/10.22785/kalf.2023.28.2.155.

Lee, S., Issues Regarding SPC's Borrowing from Its Shareholders in PPP Projects, Sogang Journal of Law and Business, Vol. 12, No. 1, pp. 3-31, 2022, https://doi.org/10.35505/sjlb.2022.4.12.1.3.

10.35505/sjlb.2022.4.12.1.3

Moon, S., Shin, J., and Yoon, K., Economic Evaluation of Large-Scale Offshore Wind Farm considering Wind Speed and Wind Turbine Capacity, The Transactions of the Korean Institute of Electrical Engineers, Vol. 70, No. 7, pp. 953-960, 2021, https://doi.org/10.5370/KIEE.2021.70.7.953.

10.5370/KIEE.2021.70.7.953

Lee, K. and Ko, K., Estimation of LCOE Ranges and Analysis of Cost Components for Korean Fixed-Bottom Offshore Wind Farms, Journal of the Korean Solar Energy Society, Vol. 43, No. 4, pp. 55-66, 2023, https://doi. org/10.7836/kses.2023.43.4.055.

10.7836/kses.2023.43.4.055

Pham, T., Im, S., and Choung, J., Prospects and Economics of Offshore Wind Turbine Systems, Journal of Ocean Engineering and Technology, Vol. 35, No. 5, pp. 382-392, 2021, https://doi.org/10.26748/KSOE.2021.061

10.26748/KSOE.2021.061

Artigao, E., Vigueras-Rodríguez, A., Honrubia-Escribano, A., Martín-Martínez, S., and Gómez-Lázaro, E., Wind Resource and Wind Power Generation Assessment for Education in Engineering, Sustainability (Switzerland), Vol. 13, pp. 1-27, 2021, https://doi.org/10.3390/su13052444.

10.3390/su13052444

Kim, B., Lee, K., Ko, K., and Choi, J., Offshore Wind Resource Assessment off the Coast of Daejeong, Jeju Island Using 30-year Wind Estimates, Scientific Reports, Vol. 12, 2022, https://doi.org/10.1038/s41598-022- 18447-7.

10.1038/s41598-022-18447-735986166PMC9391412

Lee, K., Kim, E., and Ko, K., Feasibility Study of Energy Self-Sufficiency on Chuja Island, Korea Using Wind Energy, IJRER, Vol. 9, No. 3, pp. 1224-1231, 2019, https://doi.org/10.20508/ijrer.v9i3.9532.g7698.

10.20508/ijrer.v9i3.9532.g7698

Yu, I., Recent Engineering Economy, Hyungseul Publishing, Paju, Republic of Korea, 2009.

Kim, K. and Jang, I., Study on a Development Model of Wind Power Generation Integrating an Artificial Neural Network, Journal of the Korean Society of Mineral and Energy Resources Engineers, Vol. 60, No, 4, pp. 231-241, 2023, https://doi.org/10.32390/ksmer.2023.60.4.231.

10.32390/ksmer.2023.60.4.231

Tyler, S., Patrick, D., and Daniel, H., Cost of Wind Energy Review: 2024 Edition, National Renewable Energy Laboratory (NREL), Golden, CO, United States, 2024.

Tyler, S., Patrick, D., and Daniel, H., 2022 Cost of Wind Energy Review, National Renewable Energy Laboratory (NREL), Golden, CO, United States, 2023.

Fuchs, R., Zuckerman, G. R., Duffy, P., Shields, M., Musial, W., Beiter, P., and Bredenkamp, S., The Cost of Offshore Wind Energy in the United States From 2025 to 2050, No. NREL/TP-5000-88988, National Renewable Energy Laboratory (NREL), Golden, CO, United States, 2024.

10.2172/2433785

Seo, H., B, S., Yun, D., Yu, J., and Jung, S., Korean Offshore Wind Electrical Power Generation: Current Status and Prospects, Journal of Korean Society of Environmental Engineers, Vol. 46, No. 7, 2024, https://doi. org/10.4491/KSEE.2024.46.7.382

10.4491/KSEE.2024.46.7.382

Korea Hydrographic and Oceanographic Agency, Ocean Data in Grid Framework. http://www.khoa.go.kr/. last accessed on the 8^th January 2025.

Wang, L., Kolios, A., Liu, X, Venetsanos, D., and Cai, R., Reliability of Offshore Wind Turbine Support Structures: A State-Of-The-Art Review, Renewable and Sustainable Energy Reviews, Vol. 161, 12250, 2022, https://doi.org/10.1016/j.rser.2022.112250.

10.1016/j.rser.2022.112250

Lee, K., Yang, K., and Ko, K., Correlation Analysis for LCOE and Cost Components with Terrain Complexity for Korean Onshore Wind Farms, Journal of the Korean Solar Energy Society, Vol. 44, No. 2, pp. 27-36, 2024, https://doi.org/10.7836/kses.2024.44.2.027.

10.7836/kses.2024.44.2.027

Korea Energy Agency, Competitive Bidding Announcement for Wind Production Fixed-Price Contracts in 2024, 2024. https://www.knrec.or.kr/. last accessed on the 8^th January 2025.

Gaertner, E., Rinker, J., Sethuraman, L., Zahle, F., Anderson, B., Barter, G., and Viselli, A., IEA Wind TCP Task 37: Definition of the IEA 15-megawatt Offshore Reference Wind Turbine, National Renewable Energy Laboratory (NREL), Golden, CO, United States, 2020.

10.2172/1603478

Larsén, X. G., Davis, N., Hannesdóttir, Á., Kelly, M., Svenningsen, L., Slot, R., and Floors, R., The Global Atlas for Siting Parameters Project: Extreme Wind, Turbulence, and Turbine Classes, Wind Energy, Vol. 25, No. 11, pp. 1841-1859, 2022, https://doi.org/10.1002/we.2771.

10.1002/we.2771

Journal of the Korean Solar Energy Society ISSN:1598-6411(Print) 2508-3562(Online) 한국태양에너지학회 논문집

Preview

Estimation of Variability in Internal Rate of Return for Korea Offshore Wind Projects with Financing Conditions

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Table 1.

Summary for Korean offshore wind farm and NREL data

Fig. 1.

CapEx in accordance with distance from shore and water depth

Fig. 2.

Power curve of IEA 15 MW wind turbine

Fig. 3.

Wind speeds, Weibull A and K parameters at 150 m height from GASP

Table 2.

Analysis assumption

Fig. 4.

Boxplot by gearing (a), loan period (b) and interest rate (c)

Fig. 5.

Trends of IRR with gearing and loan periods

Fig. 6.

Trends of IRR with gearing and interest rates

Fig. 7.

Trends of total tax and interest payment with loan periods over 20 years

Fig. 8.

Impact of gearing on IRR with financial risk

Acknowledgements

References