1. 서 론

육상풍력발전기와 달리 해상풍력발전기는 날씨에 따라 접근성이 크게 달라진다. 풍속이 높은 시기에는 파도의 높이도 함께 높으므로 이 시기에 해상풍력발전기에 고장이 발생하면 적시에 유지보수를 수행할 수 없다. 풍력발전단지 운영사는 가동률을 높이는 것 이외에도 고장 등의 예상치 못한 유지보수 상황을 피하기 위해 노력한다¹⁾.

풍력에너지가 다른 에너지원보다 높은 경쟁력을 갖기 위해 개발되어야 하는 요소는 다음과 같다: 가동률, 신뢰성, 효율, 적합성²⁾. 이 중 가동률과 신뢰성은 구조건전성 모니터링(structural health monitoring, SHM) 기술을 통하여 담보될 수 있다³⁾. 구조건전성 모니터링 기술의 핵심은 센싱 기술과 분석 알고리즘이다. 구조건전성 모니터링으로 획득한 정보는 상태기반정비(condition-based maintenance, CBM)에 사용된다⁴⁾. 구조건전성 모니터링은 센서로부터 지속적으로 계측되는 신호를 기반으로 작동한다. 그러나 해상풍력발전기는 접근성이 낮아 센서가 고장날 경우 적시에 수리하기에 어려움이 따른다.

해상풍력의 경우, 센서의 오차나 내구성, 데이터 획득과 전송에 더 많은 고려가 요구된다⁵⁾. 풍력발전기가 가동하는 동안 피로하중은 계속 누적된다. 센서 고장 등에 의한 데이터 손실은 피로하중 계산에 정확성을 담보할 수 없게 한다. 본 연구에서는 특정 센서 신호를 다른 신호들을 이용하여 예측하는 방법을 다룬다. 이를 통해 구조건전성 모니터링에 필요한 센서 수를 줄일 수 있고 센서 이상이 발생한 경우에도 피로하중을 파악할 수 있다. 일례로 특정 터빈에 많은 센서를 설치하여 수개월간 데이터를 측정한 후 연관성을 파악하고 나면, 동일한 터빈에 대하여는 최소의 센서 만으로도 많은 부품의 피로하중을 파악할 수 있다.

피로하중은 계측신호를 기반으로 계산된다. 계측신호의 개수가 많으면 이를 이용하는 알고리즘 또한 복잡해진다. 이런 경우 블랙박스 방식이 신호 연결 구조를 파악하는데 도움이 되는데, 이 방식을 기계학습(machine learning)이라 부른다⁶⁾. 기계학습 중 식별된 학습 데이터로부터 알고리즘을 얻는 방식을 지도학습(supervised learning)이라 부른다⁷⁾. 지도학습에서 학습 데이터는 입력 데이터와 출력 데이터로 나뉜다. 지도학습은 학습 데이터로부터 만들어지는데 다음의 두 단계를 거친다⁸⁾. 첫 번째 단계는 학습 데이터로부터 분류 모델(classification model)을 만드는 것이다. 이 과정은 학습 단계라 부른다. 두 번째 단계는 분류 모델을 테스트하는 것으로, 테스트 데이터는 학습 데이터와 구분되어야 한다. 이 과정은 테스트 단계라 부른다. 만일 학습 모델이 정확하다면 이 모델은 새로운 데이터에도 결과를 잘 도출할 것이다. 만일 학습 모델이 정확하지 않은 경우에는 만족스러운 결과가 나올 때까지 학습 알고리즘을 반복하여 수정한다.

2. 피로하중 예측 방법

특정 신호의 일부 데이터가 유실된 경우 이를 다른 여러 개의 신호값으로부터 구하는 일반적인 방식은 다항식 곡선 접합 방법(polynomial curve fitting)이다. 풍력발전기의 경우 많은 신호가 센서와 제어기로부터 취득된다. 기계학습 알고리즘은 이 신호들이 유실된 데이터 예측에 사용될 수 있도록 한다. 본 논문에서는 세 가지의 기계학습 알고리즘이 제시된다. 결정 트리 방법(decision tree), 정규 선형 회귀(regularized linear regression), 그리고 인공신경망(artificial neural network)이다. 기계학습의 대표적인 방식인 서포트 벡터 머신(support vector machine)도 시도하였으나 예측 정확도가 높지 못하여 본 논문에 포함하지 않았다. 위의 세 가지 기계학습 알고리즘의 성능을 비교하기 위하여 통계적 방법인 다항식 곡선 접합 방법(polynomial curve fitting) 방법이 함께 제시되었다.

측정 데이터는 MW급의 상용 풍력발전기로부터 계측되었다. 다음 채널들의 1분 평균, 최소, 최대, 표준편차 값이 이용되었다. 측정 채널의 단위는 출력은 [W], 풍속은 [m/s], 그 외는 [Nm]이다.

- 출력

- 풍속

- 블레이드의 루트부의 평활방향 모멘트(flapwise bending moment)

- 블레이드의 루트부의 날방향 모멘트(edgewise bending moment)

- 블레이드의 미들부의 날방향 모멘트

- 메인 샤프트의 경사 모멘트(tilt moment)

- 메인 샤프트의 요잉 모멘트(yaw moment)

- 메인 샤프트의 회전좌표계 경사 모멘트

- 메인 샤프트의 회전좌표계 요잉 모멘트

- 메인 샤프트의 토션(torsion)

- 타워 상단부의 앞뒤방향 모멘트(normal moment)

- 타워 상단부의 좌우방향 모멘트(lateral moment)

- 타워 미들부의 앞뒤방향 모멘트

- 타워 미들부의 좌우방향 모멘트

- 타워 하단부의 앞뒤방향 모멘트

- 타워 하단부의 좌우방향 모멘트

풍속은 나셀이 아니라 기상탑에서 측정한 데이터를 이용하였다. IEC 61400-13 (2015) 규정에 맞추어 블레이드의 루트부는 원통형 모양인 곳에, 블레이드 미들부는 전체 길이의 30% ~ 50% 사이에 센서를 설치하였다. 타워 상단부, 미들부, 하단부 또한 타워 아랫면에서 상부 20% 이내, 30% ~ 70% 사이, 하부 20% 이내에서 측정하였다. 블레이드의 미들부의 평활방향 모멘트는 데이터가 손실되어 제외하였다. 위 신호 중 출력과 풍속을 제외한 값은 기계 하중이다. 따라서 기계 하중 신호의 피로하중(등가하중, damage equivalent load, DEL)도 함께 계산하였다. 각 채널별 물성치(inverse S-N slope)는 아래 표에 있다.

피로하중은 다음 수식을 이용하여 구하였다.

여기에서, Req ：피로 하중(Nm)

Ri ：피로 하중 스펙트럼의 _i번째 부류에 해당하는 하중

ni ：피로 하중 스펙트럼의 i번째 부류에 해당하는 사이클 수

neq ：등가 사이클 수

m ：관련 재료에 대한 S－N 곡선의 기울기(Table 1 참조)

3. 피로하중 예측 방법 비교

본 단원에서는 네 가지 예측방식인 다항식 곡선 접합(polynomial curve fitting), 결정 트리 방법(decision tree), 정규 선형 회귀(regularized linear regression), 인공신경망(artificial neural network)을 이용한 예측 결과를 제시하였다.

3.1 다항식 곡선 접합 (polynomial curve fitting)

다항식 곡선 접합 방법은 출력 y의 평균값과 입력 x 사이의 관계식을 의미하며 출력 y는 다음과 같이 입력 x의 n차 다항식으로 표현된다.

여기에서 ε은 수식의 나머지이며 β₀, β₁, ...β_n 은 다항식의 미지변수이다. 미지변수를 찾기 위해 다항식 곡선 접합 방법은 최소자승법(least squares method)을 사용한다. 최소자승법은 나머지 ε의 제곱의 합을 최소화하는 방식이다.

본 연구에서 출력값 y는 기계하중의 1 Hz 등가하중(damage equivalent load)이다. 입력 x는 y와의 상관도가 가장 높은 변수로 정한다. Fig. 1은 1 Hz 블레이드 평활방향 등가하중과 다른 측정 채널들 사이의 상관관계를 보여준다. 가장 높은 상관관계를 갖는 변수는 타워상단부 앞뒤방향 모멘트의 등가하중값이다. 따라서 이 값을 다항식 곡선 접합 방법의 입력 x로 정한다. 각 채널별로 가장 높은 상관관계를 갖는 변수와 수치는 Table 2에 제시되어 있다.

Fig. 1

Correlation coefficients between flapwise fatigue (m = 10) and other signals

다항식의 차수는 1차 ~ 10차를 테스트하였다. 이 중 10차 함수일 때 평균제곱오차(mean square error)가 최소가 되었다. Fig. 2에서 분홍색 계측 데이터의 중간에 파란색 근접 데이터가 위치한 것을 볼 수 있다. 블레이드 루트부 평활방향 등가하중의 다항식 곡선 접합식은 다음과 같다.

위 수식에 따른 다항식 곡선 접합 방식으로 블레이드 루트부 1 Hz 평활방향 등가하중을 구한 데이터는 Fig. 3의 왼쪽에 나타나 있다. 분홍색 점은 측정값, 파란색 점은 다항식 곡선 접합 방식에 의한 예측값이다. 예측 오차의 히스토그램은 Fig. 3의 오른쪽에 제시되었다.

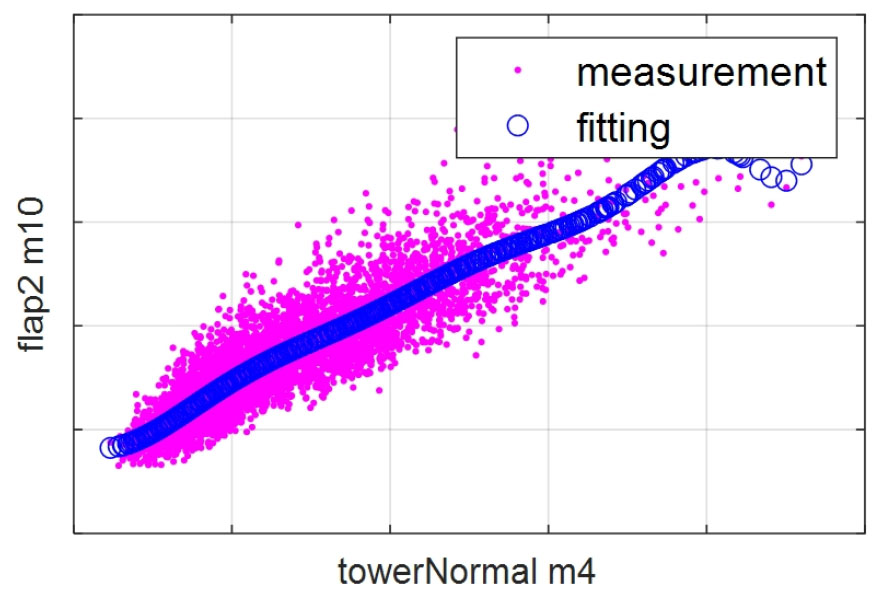
Fig. 2

Curve fitting of a blade root 1 Hz DEL flapwise bending moment (m = 10) to 1 Hz DEL tower top normal moment (m = 4)

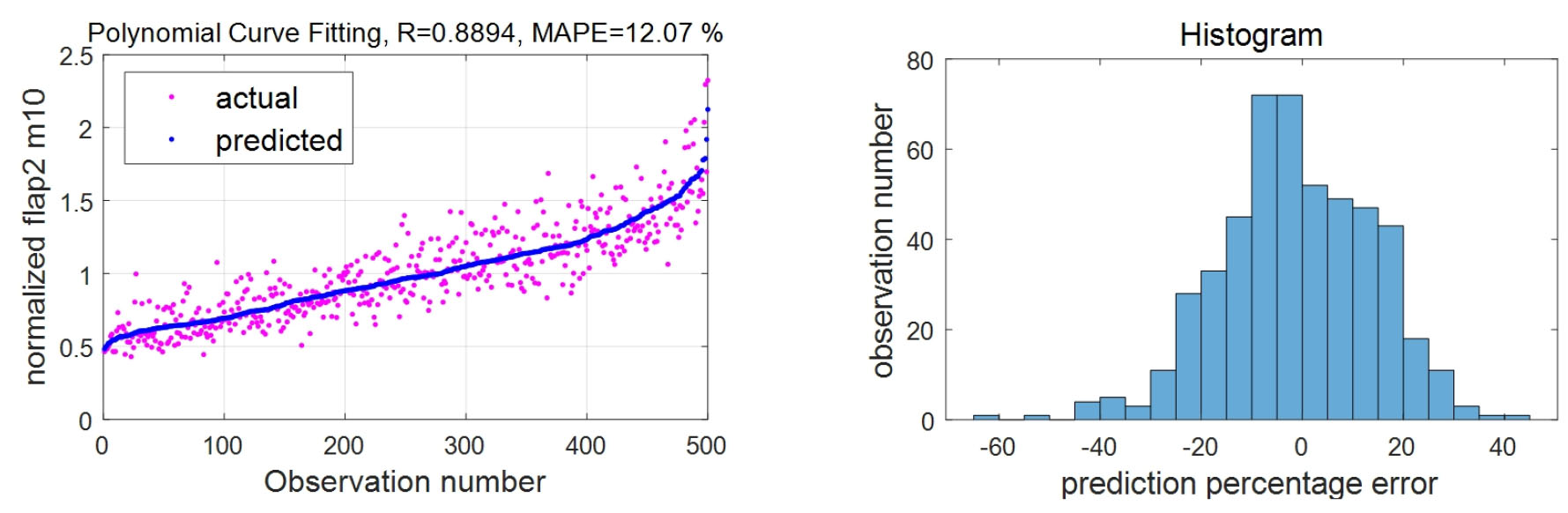
Fig. 3

Actual measurement data and predicted data (left) and histogram of prediction percentage error (right) with polynomial curve fitting for a blade root 1 Hz DEL of flapwise bending moment

Table 2의 상관관계가 높다면 Table 3의 예측 오차는 작아야 한다. 본 관계는 Fig. 4에 묘사되어 있다. 상관관계와 예측 오차 사이의 선형 추세선 수식은 다음과 같다.

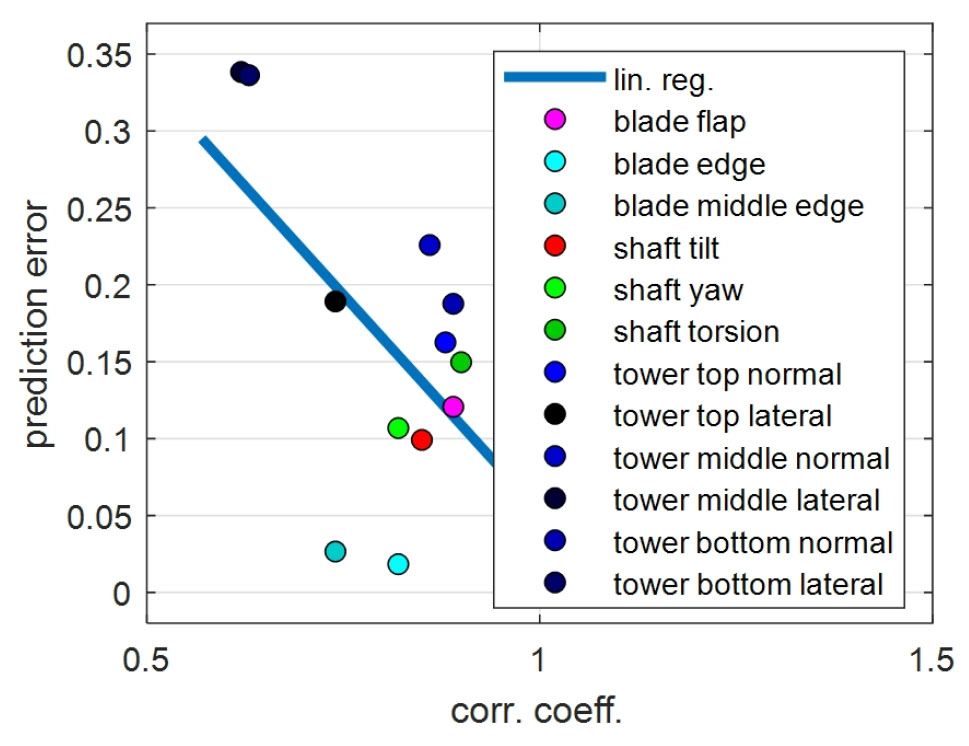
Fig. 4

Relation between correlation coefficient of the reference data and prediction error of the test data (dot), linear regression (line)

3.2 결정 트리

결정 트리 방식은 다른 기계학습과 마찬가지로 데이터를 분류한다. 결정 트리에서 데이터 분류는 매 단계마다 “결정” 과정을 통하여 이루어진다⁹⁾.

블레이드 평활방향의 1 Hz 등가하중을 이용한 에측 오차 그래프와 오차 히스토그램은 Fig. 5에 제시되어 있다. 결정 트리를 이용한 각 채널별 예측 오차는 Table 4에 기록되었다.

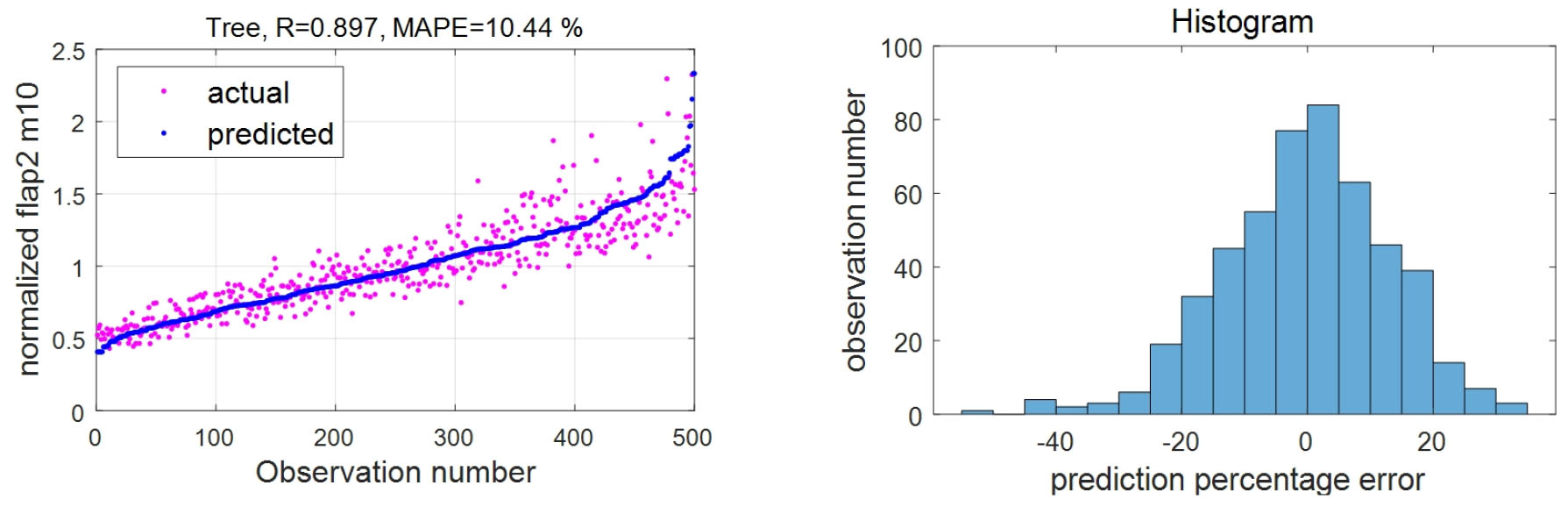
Fig. 5

Actual measurement data and predicted data (left) and histogram of prediction percentage error (right) with decision tree for a blade root 1 Hz DEL of flapwise bending moment

3.3 정규 선형 회귀

정규 선형 회귀법(regularized linear regression)은 다음 수식과 같이 1차방정식 형태를 갖는다.

X는 측정값, Y는 출력값, β는 파라미터 벡터, ε은 노이즈이다.

최적의 β를 찾기 위해 손실함수(loss function)를 이용하는데, 이 함수는 Y-X∙β와 같다. 손실함수의 최소값은 LASSO, Group-LASSO, 최소절대편차추정법(least absolute deviation method) 등을 이용하여 구한다¹⁰⁾.

정규 선형 회귀법을 이용한 예측 오차 그래프는 Fig. 6의 왼편에 제시되어 있고 히스토그램은 Fig. 6의 오른편에 있다. 본 방식을 이용한 예측 오차는 Table 5에 기록되었다.

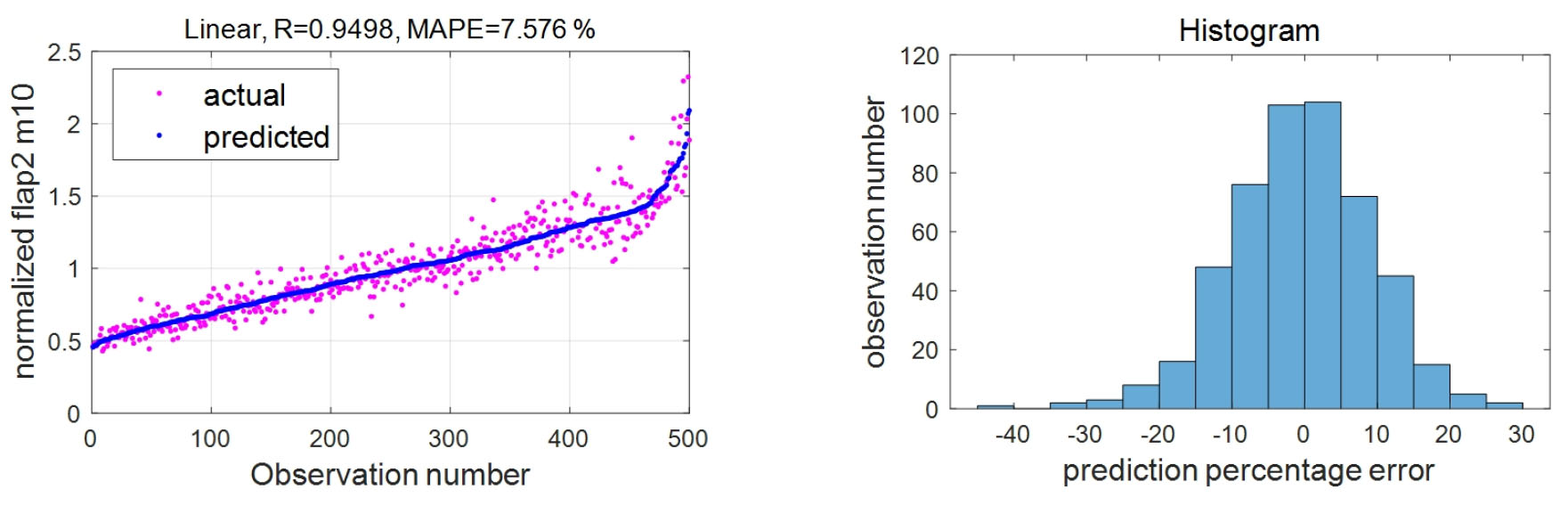
Fig. 6

Actual measurement data and predicted data (left) and histogram of prediction percentage error (right) with linear regression for a blade root 1 Hz DEL of flapwise bending moment

3.4 인공 신경망

인공 신경망(artificial neural network)은 동물 뇌의 신경 활동을 모방하는 기계학습 방법이다. 인공 신경망은 스스로 복잡한 패턴을 조직한다. 인공신경망의 노드는 층별로 배열되고 다른 층의 노드와 연결된다. 뇌 구조와 비교하면, 인공 신경망의 노드는 뇌의 신경세포이고 노드간의 연결은 뇌의 시냅스에 해당한다¹¹⁾. 뇌는 시냅스의 강도를 조정하면서 배운다. 동일한 방식으로 인공 신경망은 노드간의 가중치(weight)를 조정하며 학습한다. 따라서 인공 신경망의 학습은 가중치를 바꾸어가며 최적의 결과를 찾는 과정이다.

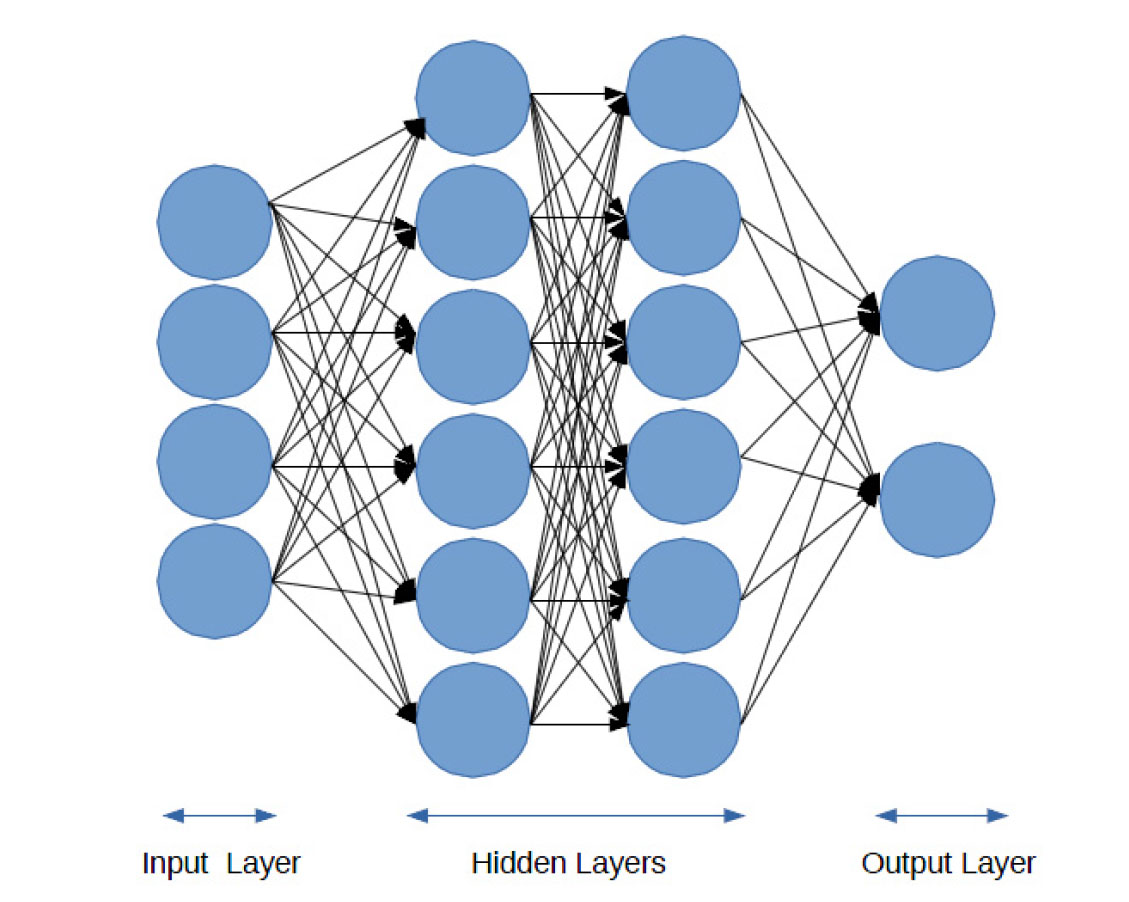
Fig. 7

Diagram of an artificial neural network¹²⁾

인공 신경망의 예측 결과와 히스토그램은 Fig. 8과 같다. 예측 오차값은 Table 6에 제시되었다.

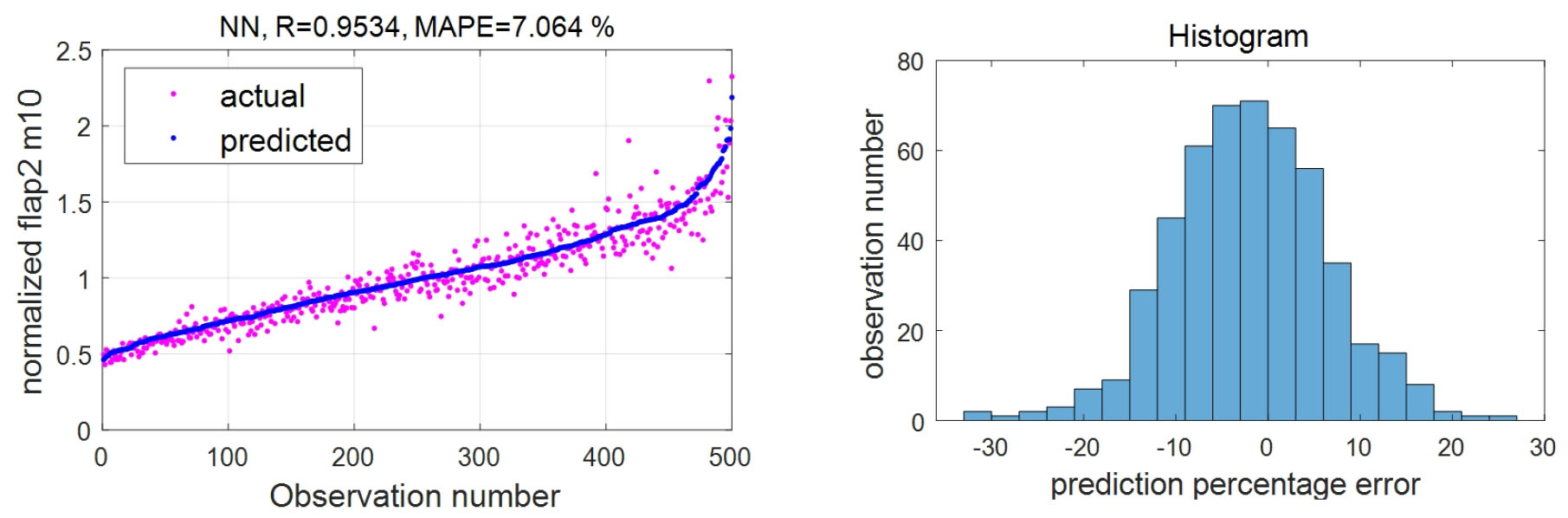
Fig. 8

Actual measurement data and predicted data (left) and histogram of prediction percentage error (right) with polynomial curve fitting for a blade root 1 Hz DEL of flapwise bending moment

3.5 회귀 분석 방식에 따른 예측 오차 비교

3.1 ~ 3.4에서 네 가지 타입의 회귀 분석 방식이 제시되었다. 각 부품 하중별 예측 오차는 Table 7에 요약되었다. 총 12개의 채널이 비교 대상으로 이용되었는데, 12개 모두 가장 높은 예측 정확도를 갖는 방식은 인공 신경망이었다. 그 다음은 12개 모두 2위를 한 정규 선형 회귀법이었다. 3위는 결정 트리인데, 메인샤프트 경사 모멘트의 경우는 다항식 곡선 접합 방식이 결정 트리보다 높은 정확도를 보였다. 결정 트리는 11개 채널에서 3위, 1개 채널에서 4위를 기록하였다. 가장 예측 정확도가 낮은 방식은 다항식 곡선 접합 방식이었다. 알고리즘 구조가 가장 복잡하고 연산시간도 오래 걸리는 인공 신경망이 가장 높은 정확도를 보였고 오랜 기간 사용되어 온 통계적 방법인 다항식 곡선 접합 방식이 가장 낮은 정확도를 나타내었다.

4. 결 론

피로하중은 MW급 풍력발전기에서 직접 측정한 데이터를 기반으로 계산하였다. 특정 채널의 피로하중을 에측하기 위하여 다음의 네 가지 방법이 이용되었다: 다항식 곡선 접합, 결정 트리, 정규 선형 회귀, 인공 신경망. 가장 높은 정확도를 보인 방식은 인공 신경망이고 그 다음으로는 정규 선형 회귀와 결정 트리 방식이었다. 따라서 기계 학습을 이용한 예측이 통계적 방식인 다항식 곡선 접합보다 우수한 성능을 보임을 알 수 있었다.

구조건전성 모니터링 중 다른 신호들을 이용한 피로하중 예측 방법을 이용하여 센서의 개수를 줄일 수 있고 센서의 고장에도 대처할 수 있다. 피로하중 예측에 기계학습을 적용하여 예측 정확도를 크게 높일 수 있다.